【Julia】ロジスティック回帰をやる
こんにちは。今回は、Juliaでロジスティック回帰を実装してみようという回です。今まではRを使ってきましたが、つい3日前くらいに唐突に「Julia始めてみようかな〜」と思い立って触り出しまして、その練習というか備忘録がてらブログにしてみました。実際にロジスティック回帰をJuliaでやろうとするならばGLMなるパッケージがあるそうですが、よくわからんかった（というよりはドキュメントを読むのが面倒だった）ので自力でやってみました。ただ、ロジットに関する実装系の日本語ブログはほとんどなかったので、後学のためにも記録として残しておきます。
準備
まずは、以下のパッケージを読み込みます。
# Load packages using Optim # optimization using Distributions # RNG using NLSolversBase # calculation of Hessian using Random using LinearAlgebra # Seed setting Random.seed!(0)
次に、いくつかの補助的な関数を定義します。頭がRに冒されているので、とりあえずRライクな関数を作りました。
rnorm(N, mu = 0, sd = 1) = rand(Normal(mu, sd), N) # Normal random variates runif(N, min = 0, max = 1) = rand(Uniform(min, max), N) # Uniform random variates plogis(x) = exp(x) / (1 + exp(x)) # Logit
それでは、今回使用するデータを擬似的に作成します。今回は二変数による回帰分析用のデータを作成していこうと思います。サイズは1000にして、二つの変数$x_{i1}$と$x_{i2}$はそれぞれ$N(0, 25)$と$U(0, 1)$から生成されるとし、誤差項$\varepsilon_{i}$は$N(0, 1)$から生成します。係数値$\beta$は長さ3の列ベクトルで、$[-3, -1, 2]$と定義します。また、結果変数の$Y_i$は確率$\text{logit}^{-1}(x_i^\top\beta + \varepsilon_i)$のベルヌーイ分布からサンプリングします。
# Define data ## Size N = 1000 ## Coefficient beta = [-3 -1 2] ## Length of coef K = length(beta) ## N * 3 matrix of covariates (1st col is intercept) X = [ones(N) rnorm(N, 0, 5) runif(N)] ## Linear aggregator y_star = X * beta' + rnorm(N) ## Calculate probability p = plogis.(y_star) ## Generate outcome variable Y = rand.(Bernoulli.(p))
対数尤度関数の定義
対数尤度関数loglikを定義します。ロジスティック回帰の場合、尤度関数$\mathcal{L}$はベルヌーイ分布として考えます。よって、対数尤度$l$は
\begin{align}
\mathcal{L} &= \prod_{i=1}^N p^{Y_i}(1-p)^{(1 - Y_i)} \\
l &= \log \mathcal{L} = \sum\limits_{i=1}^N Y_i \log(p) + (1 - Y_i) \log(1 - p)
\end{align}
となります。しかしながら、JuliaのOptim.optimize関数は何だか最小化問題を解くのが通例となってるぽい（？）のでそれに合わせた形で対数尤度関数を定義しなければなりません。とはいえ、単純に符号を反転させればOKです。
# Log-likelihood function loglik(x, y, b) len = length(y) prob = plogis.(x * b) llike = log.(prob) .* y + log.(ones(len) - prob) .* (ones(len) - y) return(-sum(llike)) # Minimization problem end
最適化
いよいよ、最適化です。その前に、分散共分散行列の計算で用いるへシアンを計算するためにTwiceDifferentiableという関数を実行します。1項目は任意の関数、2項目は初期値、3項目のautodiff = :forwardは自動微分の設定です。その後、optimizeで最適化します。このとき、Nelder-Mead法を用いました。
# For Hessian fn = TwiceDifferentiable(vars -> loglik(X, Y, vars[1:K]), ones(K); autodiff = :forward); # Optimize opt = optimize(fn, ones(K), method = NelderMead())
実行が終わったので、収束しているか確認すると
Optim.converged(opt)
true
無事、収束してました。
結果
早速、得られた計数値を取得し、またへシアンを取得して標準誤差を求めます。へシアンの符号を反転させて逆行列を取ると分散共分散行列が得られるので、その対角成分の平方根を取れば標準誤差が求まります。
# Extract the result beta_hat = Optim.minimizer(opt) # Calculate Hessian H = hessian!(fn, beta_hat) # Standard error sd = sqrt.(H |> inv |> diag)
次にパラメータの95%信頼区間を求めてみましょう。見にくいので、小数点第4位以下を切り捨てます。
# 95% CI q_ci = quantile(Normal(0, 1), [0.975]) # 1.96 upr = beta_hat + sd .* q_ci # Upper upr = round.(upr, digits = 3) lwr = beta_hat - sd .* q_ci # Lower lwr = round.(lwr, digits = 3)
以上をまとめた表を出力してみます（DataFrame形式ですが）。
using DataFrames re(x, y) = repeat([x], y) ci = map(string, re("[", 3), lwr, re(", ", 3), upr, re("]", 3)) var_name = ["Intercept", "x1", "x2"] rename(DataFrame(hcat(var_name, beta_hat, ci, sd), :auto), :x1 => "Variable", :x2 => "Est.", :x3 => "95% CI", :x4 => "Std.Error")
3×4 DataFrame
Row │ Variable Est. 95% CI Std.Error
│ Any Any Any Any
─────┼───────────────────────────────────────────────────
1 │ Intercept -2.90563 [-3.475, -2.336] 0.29058
2 │ x1 -0.839131 [-0.953, -0.726] 0.0578705
3 │ x2 2.25445 [1.451, 3.058] 0.409948
なかなか良い推定値なのではないでしょうか。実際の値である$[-3, -1, 2]$に近く、しっかりと実装できてそうです。しかしながら、少々不安なのでRでも確かめることにしました。まず、Juliaで使用したデータを書き出しちゃいましょう。
using CSV d = rename(DataFrame(hcat(Y, X), :auto), :x1 => :Y, :x2 => :Intercept, :x3 => :x1, :x4 => :x2) d |> CSV.write("d.csv", delim = ',', writeheader = true)
それでは、実際にglmでロジットを回してみます。
d <- read.csv('d.csv') summary(glm(Y ~ x1 + x2, data = d, family = 'binomial'))
Call:
glm(formula = Y ~ x1 + x2, family = "binomial", data = d)
Deviance Residuals:
Min 1Q Median 3Q Max
-3.4804 -0.3232 -0.0565 0.2520 2.6856
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -2.90562 0.29058 -9.999 < 2e-16 ***
x1 -0.83913 0.05787 -14.500 < 2e-16 ***
x2 2.25441 0.40995 5.499 3.81e-08 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 1312.48 on 999 degrees of freedom
Residual deviance: 515.87 on 997 degrees of freedom
AIC: 521.87
Number of Fisher Scoring iterations: 7
グッドですね。ほとんど推定値がドンピシャでした。きちんと動かせましたね。
予測確率の計算
最後に、せっかくなので変数$x_{2i}$を用いた予測確率を計算していきたいと思います。ここでのアプローチは、King, Tomz & Wittenberg (2000, AJPS)*1が提案したシュミレーションを用いたprocedureであるCLARIFYを利用して、予測確率を計算します。手順は
- モデルの推定値・分散を用いて多変量正規分布からランダムに変数をサンプリング
- 興味がある説明変数以外は中央値（または平均値）に固定した擬似的な説明変数の行列を作成
- 1と2から予測確率の行列を計算し、点推定値と95%信頼区間を求める
です。そこまで難しくはないのでちゃっちゃっとやります。
# MVnormal rng rmvnorm(N, mu, sigma) = rand(MvNormal(mu, sigma), N) b_rng = rmvnorm(N, beta_hat, sd.^2) # Generate hypothetical `x2` x2_hyp = collect(0:0.01:1) # Generate hypothetical covariate X_hyp = [ones(length(x2_hyp)) re(median(X[:, 2]), length(x2_hyp)) x2_hyp] # Calculate probability and CI EY = plogis.(X_hyp * b_rng) lower = zeros(size(EY)[1]) med = zeros(size(EY)[1]) upper = zeros(size(EY)[1]) for l in 1:size(EY)[1] lower[l] = quantile(EY[l, :], 0.025) med[l] = median(EY[l, :]) upper[l] = quantile(EY[l, :], 0.975) end # Plot using Plots plot(x2_hyp, med, ribbon = (med .- lower, upper .- med), legend=:bottomright, fa = .3, label = false, xlabel = "x2", ylabel = "Predicted probabilities", dpi = 300)
こちらも良い感じですね。すっきりと実装から可視化までスムーズにできたと思います。
おわりに
今のところ、正直言ってJuliaのご利益がいまいち分かってませんw まだRでいいかなぁとか思ったり。
【R/Rcpp】EMアルゴリズムで項目反応理論を実装する ー Polya-Gamma Data Augmentationの応用
こんにちは。前回・前々回と項目反応理論（Item Response Theory, IRT）のスクラッチ実装に関する記事でしたが、今回もその続きというか発展編です。これまではベイズ推定を用いるのが通例でしたが、やはりベイズは気長に待たなければならないという悲しい点があります。そこで、今回はより高速なEMアルゴリズムを利用して項目反応理論を速く推定してみましょう～！という内容になります。
ここでは、Polson et al. (2013)*1 らによるPolya-Gamma分布を利用したロジットモデル推定のスキームを応用していきます。彼らの論文では、Polya-Gamma分布を用いてロジットモデルでのギブスサンプリングを効率的に実現するということが提案されていました。それを応用することで、ロジットモデルでも効率的にEMアルゴリズムによる推定を行うことができるようになります。ゆっくりと解説していきます。
Polya-Gamma分布による定式化については、株式会社Nospareさんのqiita記事がより詳しいのでそちらも参照してください。 qiita.com
また、今回使用するコードはすべてGithub上にアップしてますので、そちらも併せてご覧ください。
セットアップ
まずは前回と同様にIRTモデルのセットアップから行います。被験者 $i=1,...,I$と問題$j=1,...,J$があるとします。この時、$i$が$j$で正解する（$y_{ij}=1$, otherwise $0$）確率を以下で定義します：
\begin{equation}
\text{Pr}(y_{ij}=1) = \frac{\exp(\psi_{ij})}{1 + \exp(\psi_{ij})}, \ \ \ \psi_{ij} = \alpha_j + \beta_j \theta_i
\end{equation}
ここで、$\alpha_j, \beta_j$はそれぞれ問題$j$の解答困難度・識別度であり、$\theta_i$は被験者$i$の能力です。上記のモデルに対してベイズ推定などを用いることで潜在的なパラメータである$\alpha_j, \beta_j, \theta_i$を推定します。
仮に上記のモデルをベイズ推定する場合、事後分布が上手く定まらないのでMetropolis Hastingsアルゴリズムなどに頼る必要があります。しかし、これはギブスサンプリングに比べると非効率であり、そのためギブスサンプリングが簡単に行える別の二項選択モデルであるプロビットモデルが好まれていました*2。しかし、Polson et al. (2013)が提案したPolya-Gamma data augmentationのスキームを用いれば、プロビットモデルと同様に簡単に効率的なギブスサンプラーを構築できるのです。
Polya-Gamma data augmentationを利用したIRTモデルの推定
ここからは、Goplerud (2019) *3 によるPolya-Gamma分布を用いたIRTの定式化に従っていきます。まず、最初にPolya-Gamma分布の定義を見ていきます。以下の場合、確率変数$X$は$b>0, c\in \mathop{\mathbb{R}}$を持つPolya-Gamma分布に従うとします ($X\sim PG(b, c))$：
\[X = \frac{1}{2\pi^2}\sum\limits_{k=1}^{\infty}\frac{g_k}{(k - 1/2)^2 + c^2/(4\pi^2)}\]
また、$g_k \sim Ga(b, 1)$です。ここでIRT式について、$\psi_{ij} \in \mathop{\mathbb{R}}$で$\omega_{ij} \sim PG(1, 0)$の場合：
\[
\frac{\exp(\psi_{ij})^{y_{ij}}}{1 + \exp(\psi_{ij})}= \frac{1}{2}\exp (k_{ij}\psi_{ij}) \int\limits_{0}^{\infty} \exp(-\omega_{ij}\psi_{ij}^2/2) f(\omega_{ij}) d\omega_{ij}, \ \ \ k_{ij} = y_{ij} - 1/2
\]
として書くことができます。この場合、Polya-Gammaの確率変数$\omega_{ij}$によるdata augmentationを行った後の完全データ尤度関数$f(y_{ij}, \omega_{ij}\mid \alpha_j, \beta_j, \theta_i)$は
\[f(y_{ij}, \omega_{ij}\mid \alpha_j, \beta_j, \theta_i) \propto \exp\left(k_{ij}\psi_{ij} - \frac{\omega_{ij}(\psi_{ij})^2}{2}\right) f(\omega_{ij}\mid 1, 0)\]
となります。パラメータに対して正規分布を事前分布として定めることで、事後分布も正規分布として得ることができるためギブスサンプリングが可能となります。めっちゃ便利ですね。ちなみに、Polya-Gamma data augmentationを使ってIRTのギブスサンプリングをしている例がJiang & Templin (2019) の研究です*4。しかし、今回はEMアルゴリズム実装に興味があるので、ギブスサンプリングの詳細は省きます。
EMアルゴリズムへの応用
次に、Polya-Gamma分布を用いた拡大法のEMアルゴリズムへの適用の仕方を見ていきます。まず、パラメータの事前分布を
\[\alpha_j \sim N(\alpha_0, A_0), \ \ \ \beta_j \sim N(\beta_0, B_0), \ \ \ \theta_i \sim N(0, 1)\]
と設定します。$\xi, \xi^*$をそれぞれ現在のイテレーション・一つ前のイテレーションのパラメータの集合とします。この場合、E-stepにおいてQ関数は以下のように求めます：
- E-step
\begin{align}
Q(\xi, \xi^*) &\propto \sum\limits_{i=1}^I\sum\limits_{j=1}^J k_{ij}\psi_{ij} - \frac{\mathop{\mathbb{E}}[\omega_{ij}\mid y_{ij}, \xi^*]\psi_{ij}^2}{2}\\\nonumber
&- \sum\limits_{i=1}^I\frac{\theta_i^2}{2} - \sum\limits_{j=1}^J \frac{(\alpha_j-\alpha_0)^2}{2A_0} - \sum\limits_{j=1}^J\frac{(\beta_j-\beta_0)^2}{2B_0}
\end{align}
また、$k_{ij} = y_{ij} - 1/2; \ \ \ \psi_{ij} = \alpha_j + \beta_j \theta_i$であり、$\omega_{ij}$の一つ前のイテレーションにおけるパラメータと観測される$y_{ij}$を条件とした場合の条件付き期待値は：
\[\mathop{\mathbb{E}}[\omega_{ij}\mid y_{ij}, \xi^*] = \frac{\tan(\psi_{ij}^*/2)}{2\psi_{ij}^*}\]
と表せます。式中の$tan$はハイパボリックタンジェントのtanhを打ちたかったのですが、はてなリンクが自動に付与されてしまう関係で数式が表示されなくなってしまうので仕方なく$tan$にしてます。タイポではないです、ご了承ください。本題に戻りますが、M-stepでは単純にQ関数を任意のパラメータについて最大化することでパラメータをアップデートするだけです。パラメータは$\theta \rightarrow \alpha \rightarrow \beta$の順にアップデートしていきます：
- M-step
その1. $\theta_i$のアップデート
\begin{align}
\frac{\partial Q}{\partial \theta_i} &= \sum\limits_{j=1}^J \beta_j^* k_{ij} - \alpha_j^*\beta_j^* \mathop{\mathbb{E}}[\omega_{ij}\mid y_{ij},\xi^*] - (\beta_j^*)^2\theta_i\mathop{\mathbb{E}}[\omega_ij\mid y_{ij},\xi^*] - \theta_i = 0\\
\therefore \theta_i &= \left(\sum\limits_{j=1}^J(\beta_j^*)^2\mathop{\mathbb{E}}[\omega_{ij}\mid y_{ij},\xi^*] + 1\right)^{-1}\left(\sum\limits_{j=1}^J \beta_j^*k_{ij} - \alpha_j^*\beta_j^*\mathop{\mathbb{E}}[\omega_{ij}\mid y_{ij},\xi^*]\right)
\end{align}
その2. $\alpha_j$のアップデート
\begin{align}
\frac{\partial Q}{\partial \alpha_j} &= \sum\limits_{i=1}^Ik_{ij}- \alpha_j\mathop{\mathbb{E}}[\omega_{ij}\mid y_{ij},\xi^*] - \beta_j^*\theta_i\mathop{\mathbb{E}}[\omega_{ij}\mid y_{ij},\xi^*] - \frac{\alpha_j - \alpha_0}{A_0}= 0\\
\therefore \alpha_j &= \left( A_0^{-1} + \sum\limits_{i=1}^I\mathop{\mathbb{E}}[\omega_{ij}\mid y_{ij},\xi^*]\right)^{-1}\left(\alpha_0A_0^{-1} + \sum\limits_{i=1}^I k_{ij} - \beta_j^*\theta_i\mathop{\mathbb{E}}[\omega_{ij}\mid y_{ij},\xi^*] \right)
\end{align}
その3. $\beta_j$のアップデート
\begin{align}
\frac{\partial Q}{\partial \beta_j} &= \sum\limits_{i=1}^I k_{ij}\theta_i - \alpha_j\theta_i\mathop{\mathbb{E}}[\omega_{ij}\mid y_{ij},\xi^*] - \beta_j \theta_i^2 \mathop{\mathbb{E}}[\omega_{ij}\mid y_{ij},\xi^*] - \frac{\beta_j-\beta_0}{B_0}=0\\
\therefore \beta_j &= \left(B_0^{-1} + \sum\limits_{i=1}^I\theta_i^2\mathop{\mathbb{E}}[\omega_{ij}\mid y_{ij},\xi^*] \right)^{-1}\left(\beta_0B_0^{-1}+\sum\limits_{i=1}^I k_{ij}\theta_i - \alpha_j\theta_i\mathop{\mathbb{E}}[\omega_{ij}\mid y_{ij},\xi^*]\right)
\end{align}
上記のE-stepとM-stepを収束するまで繰り返します。ここで、収束判断の基準については現在のパラメータと一つ前のイテレーションでのパラメータとの相関係数を用い、$\min(1 - cor(\xi, \xi^*)) < 1e-6$となる場合に収束したと判断します。
パラメトリックブートストラップによる信頼区間の導出
EMアルゴリズムは確かに速いのですが、点推定値しか求めてくれません。そこで、Lewis & Poole (2004) *5 が提案したパラメトリックブートストラップを用いて信頼区間を求めていきます。手順は以下の通りです：
元モデルでのパラメータ推定値によって予測確率を求め、ベルヌーイ分布から$\hat{y}_{ij}$をサンプリングする
$\hat{y}_{ij}$を用いて再度IRTを行い、パラメータを推定し保存。
上記を任意の回数繰り返します。これで得られた推定値を利用して信頼区間を求めます。また、信頼区間を求める際にバイアス補正を行い、具体的には任意のパラメータ$\delta$についての区間推定値を求める場合：
\[
\left[\delta_{\text{boot}}^{\text{lower}} + \hat{\delta} - \bar{\delta}_\text{boot}, \ \ \delta_{\text{boot}}^{\text{upper}} + \hat{\delta} - \bar{\delta}_\text{boot}\right]
\]
とします。ここで、$\hat{\delta}$は元モデルで得られた推定値、$\bar{\delta}_\text{boot}$はブートストラップによって得られた推定値の平均、$\delta_{\text{boot}}^{\text{lower}}$, $\delta_{\text{boot}}^{\text{upper}}$はその下側・上側パーセント点を表します。この操作をすることによって、元モデルからの推定値に対応した区間を求めることができます。
応用例：第106回連邦議会における米国上院議員の投票行動分析
今回も、{MCMCpack}パッケージに収録されているアメリカ連邦議会上院の第106議会での点呼式投票データ*6を使って各議員の理想点推定をしていこうと思います。政治学の文脈では、空間投票モデルとIRTの整合性が非常に高いので、例えば政治アクターの投票データ等を用いて彼らの潜在的な選好・イデオロギーを推定する際にIRTは頻繁に用いられています。アメリカ議会から最高裁、国際連合総会など様々な投票が起こる政治アリーナの分析では重宝されています。
アメリカ議会の投票行動を分析すると「共和党 vs. 民主党」のような議員の党派性がくっきりと表れた投票行動が為されています。それらをIRTを使ってリカバーしていこうというのがここでのモチベーションです。
実際のところ、私自身が政治学畑の人間なのでこういった投票行動の分析に関する応用が多いとは思いますが、元を辿ればIRTはテストデータ等の分析に使われるので、当然そちらの方にも適用できます。ただ、政治学の文脈だと、IRTは人々のイデオロギーを測る際に有用であり、目に見えない人の選好を見ようとする試みが気持ち悪くて結構好きです。ともあれ、早速やっていきましょう。
まずは、データを読み込みましょう。
data(Senate, package = "MCMCpack")
データを確認すると、点呼式投票 (rc~列) 以外の議員に関するデータが含まれていることがわかります。
Senate[1:10, 1:10]
id statecode state party member rc1 rc2 rc3 rc4 rc5 SESSIONS 49700 41 ALABAMA 1 SESSIONS 1 0 0 0 1 SHELBY 94659 41 ALABAMA 1 SHELBY 1 0 0 0 1 MURKOWSKI 14907 81 ALASKA 1 MURKOWSKI 1 0 0 0 1 STEVENS 12109 81 ALASKA 1 STEVENS 1 0 0 0 1 KYL 15429 61 ARIZONA 1 KYL 1 0 0 0 1 MCCAIN 15039 61 ARIZONA 1 MCCAIN 1 0 0 0 1 HUTCHINSON 29306 42 ARKANSA 1 HUTCHINSON 1 0 0 0 1 LINCOLN 29305 42 ARKANSA 0 LINCOLN 1 0 0 1 0 BOXER 15011 71 CALIFOR 0 BOXER 1 1 1 1 0 FEINSTEIN 49300 71 CALIFOR 0 FEINSTEIN 1 1 1 1 0
行名は議員の名前になっており、属する州や政党のインデックス (1 = Republican, 0 = Democrat)が入ってます。とはいえ、IRTをするうえでは不要なので全部切り捨てて、またSenateデータはデータフレームなので行列に変換します。
Y <- as.matrix(Senate[, 6:length(Senate)])
EMアルゴリズムをプログラムする
次にEMアルゴリズムを回す関数やパラメータをアップデートする関数を定義します。ここで、推定をより高速にするためにC++を利用していきます。$\texttt{R}には$RcppやRcppArmadilloといった効率的にC++を利用できる環境があるので思う存分使っていきましょう。
$\mathop{\mathbb{E}}[\omega_{ij}\mid y_{ij}, \xi^*]$を求める関数
E-stepの箇所で説明した通り、$\mathop{\mathbb{E}}[\omega_{ij}\mid y_{ij}, \xi^*]$は一つ前のイテレーションでのパラメータを基にして計算します。式とコードは以下の通りです（sourceCpp(draw_E_Omega.cpp)で読み込み）：
\[\mathop{\mathbb{E}}[\omega_{ij}\mid y_{ij}, \xi^*] = \frac{\tan(\psi_{ij}^*/2)}{2\psi_{ij}}\]
//[[Rcpp::depends(RcppArmadillo)]] #include <RcppArmadillo.h> using namespace Rcpp; using namespace arma; //[[Rcpp::export]] arma::mat draw_E_Omega(arma::vec alpha, arma::vec beta, arma::vec theta) { // Generate I length row vector filled with 1 arma::vec intercept(theta.n_rows); intercept = intercept.ones(); // 2 by J item parameter matrix arma::mat beta_tilde = join_horiz(alpha, beta).t(); // I by 2 individual parameter matrix // 1st column is intercept arma::mat Theta = join_horiz(intercept, theta); // Calculate psi arma::mat psi = Theta * beta_tilde; // Calculate E(omega) arma::mat Omega = arma::tanh(psi / 2) / (2 * psi); return(Omega); }
$\theta_i$をアップデートする関数
M-stepの箇所で紹介した通りにコードを書いていきます。式とコードは（sourceCpp(draw_theta.cpp) で読み込み）：
\[\theta_i = \left(\sum\limits_{j=1}^J(\beta_j^*)^2\mathop{\mathbb{E}}[\omega_{ij}\mid y_{ij},\xi^*] + 1\right)^{-1}\left(\sum\limits_{j=1}^J \beta_j^*k_{ij} - \alpha_j^*\beta_j^*\mathop{\mathbb{E}}[\omega_{ij}\mid y_{ij},\xi^*]\right)\]
#include <Rcpp.h> using namespace Rcpp; //[[Rcpp::export]] NumericVector draw_theta(NumericMatrix Y, NumericVector alpha, NumericVector beta, NumericMatrix Omega, int constraint) { int I = Y.nrow(); int J = Y.ncol(); NumericVector theta(I); for (int i = 0; i < I; i++) { double left_part = 0; double right_part = 0; for (int j = 0; j < J; j++) { if (NumericVector::is_na(Y(i, j))) { left_part += 0; right_part += 0; } else { double omega_ij = Omega(i, j); double k_ij = Y(i, j) - 0.5; left_part += std::pow(beta[j], 2.0) * omega_ij; right_part += beta[j] * k_ij - alpha[j] * beta[j] * omega_ij; } } left_part = left_part + 1; theta[i] = (1 / left_part) * right_part; } if (theta[constraint - 1] < 0) { theta = -theta; } return(theta); }
ここでconstraintという変数を用いることで、自分が指定したユニットの$\theta_i$が常に正の値を取るように設定してます。IRTのようなモデルでは解の符号が反転することがあるのでそれらを防ぐのに効果的かと思われます。
$\alpha_j$をアップデートする関数
$\alpha_j$も同様にしてコードを書いていきます（sourceCpp(draw_alpha.cpp) で読み込み）：
\[ \alpha_j = \left( A_0^{-1} + \sum\limits_{i=1}^I\mathop{\mathbb{E}}[\omega_{ij}\mid y_{ij},\xi^*]\right)^{-1}\left(\alpha_0A_0^{-1} + \sum\limits_{i=1}^I k_{ij} - \beta_j^*\theta_i\mathop{\mathbb{E}}[\omega_{ij}\mid y_{ij},\xi^*] \right)\]
#include <Rcpp.h> using namespace Rcpp; //[[Rcpp::export]] NumericVector draw_alpha(NumericMatrix Y, NumericVector beta, NumericVector theta, NumericMatrix Omega, double a0, double A0) { int I = Y.nrow(); int J = Y.ncol(); NumericVector alpha(J); for (int j = 0; j < J; j++) { double left_part = 0; double right_part_1 = 0; double right_part_2 = 0; for (int i = 0; i < I; i++) { if (NumericVector::is_na(Y(i, j))) { left_part += 0; right_part_1 += 0; right_part_2 += 0; } else { double omega_ij = Omega(i, j); double k_ij = Y(i, j) - 0.5; left_part += omega_ij; right_part_1 += k_ij; right_part_2 += theta[i] * omega_ij; } } left_part = left_part + 1/A0; double right_part = a0/A0 + right_part_1 - beta[j] * right_part_2; alpha[j] = (1 / left_part) * right_part; } return(alpha); }
$\beta_j$をアップデートする関数
最後に$\beta_j$の関数を書きます（sourceCpp(draw_beta.cpp) で読み込み）：
\[\beta_j = \left(B_0^{-1} + \sum\limits_{i=1}^I\theta_i^2\mathop{\mathbb{E}}[\omega_{ij}\mid y_{ij},\xi^*] \right)^{-1}\left(\beta_0B_0^{-1}+\sum\limits_{i=1}^I k_{ij}\theta_i - \alpha_j\theta_i\mathop{\mathbb{E}}[\omega_{ij}\mid y_{ij},\xi^*]\right)\]
#include <Rcpp.h> using namespace Rcpp; //[[Rcpp::export]] NumericVector draw_beta(NumericMatrix Y, NumericVector alpha, NumericVector theta, NumericMatrix Omega, double b0, double B0) { int I = Y.nrow(); int J = Y.ncol(); NumericVector beta(J); for (int j = 0; j < J; j++) { double left_part = 0; double right_part_1 = 0; double right_part_2 = 0; for (int i = 0; i < I; i++) { if (NumericVector::is_na(Y(i, j))) { left_part += 0; right_part_1 += 0; right_part_2 += 0; } else { double omega_ij = Omega(i, j); double k_ij = Y(i, j) - 0.5; left_part += std::pow(theta[i], 2.0) * omega_ij; right_part_1 += k_ij * theta[i]; right_part_2 += theta[i] * omega_ij; } } left_part = left_part + 1/B0; double right_part = b0/B0 + right_part_1 - alpha[j] * right_part_2; beta[j] = (1 / left_part) * right_part; } return(beta); }
EMアルゴリズムを回す関数
アルゴリズムを回す関数は$\texttt{R}$で定義します。なぜかというと、単純に私の力不足でC++でのコーディングができなかっただけです。コードは以下の通りです：
# Loading wrapper function ==================== pg_emirt <- function(Y, init = NULL, prior = NULL, constraint = NULL, maxit = 500, tol = 1e-6, verbose = 10) { cat("===========================================================================\n") cat("2PL Item Response Model with EM Algorithm and Polya-Gamma Data Augmentation\n") cat("===========================================================================\n") # Measuring implementation times stime <- proc.time()[3] if (is.null(init)) { cat("Initial values is not supplied, so computing from the data.....") theta_init <- as.numeric(scale(rowMeans(Y, na.rm = TRUE))) alpha_init <- beta_init <- rep() for (j in 1:ncol(Y)) { c <- suppressWarnings(coef(glm(Y[, j] ~ theta_init, family = "binomial"))) alpha_init[j] <- ifelse(abs(c[1]) > 10, 0.1, c[1]) beta_init[j] <- ifelse(abs(c[2]) > 10, 0.1, c[2]) } init <- list(theta = theta_init, alpha = alpha_init, beta = beta_init) cat("DONE!\n") } if (is.null(prior)) { cat("Prior is not supplied, so automatically setting:\n") cat("alpha ~ N(0, 100), beta ~ N(0, 100)\n") prior <- list(a0 = 0, A0 = 100, b0 = 0, B0 = 100) } # Get initial values theta <- init$theta alpha <- init$alpha beta <- init$beta # If theta constraint is not supplied if (is.null(constraint)) constraint <- which.max(theta) if (theta[constraint] < 0) theta <- -theta # Get priors a0 <- prior$a0 A0 <- prior$A0 b0 <- prior$b0 B0 <- prior$B0 # Convergence check statistics store (correlation between current and previous parameters) all_cor <- matrix(NA, maxit, 3) colnames(all_cor) <- c("alpha", "beta", "theta") # EM cat("Start EM:\n") for (g in 1:maxit) { ## Previous parameters theta_old <- theta alpha_old <- alpha beta_old <- beta ## E-step (calculate E[omega]) Omega <- draw_E_Omega(alpha_old, beta_old, theta_old) ## M-step (theta -> alpha -> beta) theta <- draw_theta(Y, alpha_old, beta_old, Omega, constraint) alpha <- draw_alpha(Y, beta_old, theta, Omega, a0, A0) beta <- draw_beta(Y, alpha, theta, Omega, b0, B0) ## Convergence stat all_cor[g, 1] <- cor(alpha_old, alpha) all_cor[g, 2] <- cor(beta_old, beta) all_cor[g, 3] <- cor(theta_old, theta) ## If converged if (min(1 - all_cor[g, ]) < tol) { ### Conv stat all_cor <- na.omit(all_cor) attr(all_cor, "na.action") <- NULL ### Parameters names(theta) <- rownames(Y) parameters <- list(alpha = alpha, beta = beta, theta = theta) ### Organize L <- list(parameters = parameters, converge = TRUE, conv_check = all_cor, iter = g, data = list(Y = Y, init = init, prior = prior, constraint = constraint, maxit = maxit, tol = tol)) ### Record time etime <- proc.time()[3] cat("Model converged at iteration", g, ": total time", round(etime - stime, 3), "sec\n") return(L) } ## If failed to converge if (g == maxit) { ### Parameters names(theta) <- rownames(Y) parameters <- list(alpha = alpha, beta = beta, theta = theta) ### Organize L <- list(parameters = parameters, converge = FALSE, conv_check = all_cor, iter = g, data = list(Y = Y, init = init, prior = prior, constraint = constraint, maxit = maxit, tol = tol)) ### Record time etime <- proc.time()[3] cat("Model failed to converge", ": total time", round(etime - stime, 3), "sec\n") warning("The result may not be reliable; return the result as it is.") return(L) } ### Print the status if (g %% verbose == 0) { mtime <- proc.time()[3] cat("Iteration", g, "eval =", min(1 - all_cor[g, ]), ": time", round(mtime - stime, 3), "sec\n") } } }
引数は以下の通りです：
Y: 解答（投票）行列init: 初期値prior: 事前分布constraint: 常に$\theta_i$が正の値を取るユニットの番号maxit: 最大イテレーション数（デフォルトは500）tol: 収束基準（デフォルトは1e-6）verbose: 何イテレーション毎にメッセージを出力するか（デフォルトは10）
パラメトリックブートストラップを行う関数
ブートストラップの関数も$\texttt{R}$で書きました：
# Loading parametric bootstrap function =================================== pg_em_boot <- function(model, boot = 100, verbose = 10) { cat("===========================================\n") cat("Parametric bootstrap for Polya-Gamma EM IRT\n") cat("===========================================\n") stime <- proc.time()[3] # For suppressing the messages quiet <- function(x) { sink(tempfile()) on.exit(sink()) invisible(force(x)) } # Extract the estimated parameters alpha <- model$parameters$alpha beta <- model$parameters$beta theta <- model$parameters$theta # Storage theta_boot <- matrix(NA, length(theta), boot) rownames(theta_boot) <- names(theta) alpha_boot <- beta_boot <- matrix(NA, length(alpha), boot) # Bootstrap for (b in 1:boot) { # Generating random binomial variates (prediction of Y) set.seed(b) p <- plogis(cbind(1, theta) %*% rbind(alpha, beta)) y_pred <- matrix(rbinom(length(theta) * length(alpha), 1, p), length(theta), length(alpha)) # Estimation fit_boot <- quiet(pg_emirt(Y = y_pred, init = model$data$init, prior = model$data$prior, constraint = model$data$constraint, maxit = model$data$maxit, tol = model$data$tol, verbose = model$data$maxit + 1)) # Saving theta_boot[, b] <- fit_boot$parameters$theta alpha_boot[, b] <- fit_boot$parameters$alpha beta_boot[, b] <- fit$parameters$beta if (b %% verbose == 0) { mtime <- proc.time()[3] cat("Bootstrap", b, "done : time", round(mtime - stime, 3), "sec\n") } } # Return the results etime <- proc.time()[3] L <- list(alpha = alpha_boot, beta = beta_boot, theta = theta_boot) cat("Bootstrap finished : total time", round(etime - stime, 3), "sec\n") return(L) }
初期値・事前分布の設定
実装するにあたり、初期値と事前分布を設定します。まずは、初期値の設定手順は以下の通りです：
投票行列に対して行ごとの平均値を計算し標準化することで$\theta_i$の初期値を得る
$\theta_i$の初期値を投票行列の各項目に対する投票（0 or 1）に回帰させる（ロジット回帰をJ回行う）
切片の推定値を$\alpha_j$の初期値、また$\theta_i$初期値の係数値を$\beta_j$の初期値とする
コードは以下の通りです：
## Generate initial values, constraint and priors =========== # Calculate the standardized value of the probability of yea response # as initial value of theta theta_init <- as.numeric(scale(rowMeans(Y, na.rm = TRUE))) # With initial value of theta, get initial values of alpha and beta # by regressing Y on theta alpha_init <- beta_init <- rep() for (j in 1:ncol(Y)) { c <- coef(glm(Y[, j] ~ theta_init, family = "binomial")) alpha_init[j] <- ifelse(abs(c[1]) > 10, 0.1, c[1]) beta_init[j] <- ifelse(abs(c[2]) > 10, 0.1, c[2]) } # Aggregate init <- list(theta = theta_init, alpha = alpha_init, beta = beta_init)
また、constraintはMCMCpack::MCMCirt1dの関数説明で紹介されている通りに従い、共和党のHELMSに定め、仮にHELMSの$\theta_i$の初期値が負の値を取っている場合には初期値全体を反転させます：
# Set constraint such that theta of HELMS always takes a positive value constraint <- which(rownames(Y) == "HELMS") if (theta_init[constraint] < 0) theta_init <- -theta_init
次に、事前分布を以下の通りに設定します：
\[\alpha_j \sim N(0, 25), \ \ \ \beta_j \sim N(0, 25), \ \ \ \theta_i \sim N(0, 1)\]
この場合、$\alpha_0=0, A_0=25, \beta_0 = 0, B_0 = 25$となります。よって：
# Priors prior <- list(a0 = 0, A0 = 25, b0 = 0, B0 = 25)
これで準備が整いました！
実装
それでは実装していきます：
## Run PG-EM IRT ============================================= model <- pg_emirt(Y = Y, init = init, prior = prior, constraint = constraint, maxit = 500, tol = 1e-6, verbose = 10)
=========================================================================== 2PL Item Response Model with EM Algorithm and Polya-Gamma Data Augmentation =========================================================================== Start EM: Iteration 10 eval = 5.770342e-05 : time 0.093 sec Iteration 20 eval = 9.77759e-06 : time 0.169 sec Iteration 30 eval = 1.749291e-06 : time 0.199 sec Model converged at iteration 35 : total time 0.215 sec
鬼高速ですねｗ 推定に0.2秒ほどしかかかりませんでした。次にブートストラップを100回ほどしていきます：
## Boostrap ================================================== boot <- pg_em_boot(model)
=========================================== Parametric bootstrap for Polya-Gamma EM IRT =========================================== Bootstrap 10 done : time 1.36 sec Bootstrap 20 done : time 2.455 sec Bootstrap 30 done : time 3.541 sec Bootstrap 40 done : time 4.685 sec Bootstrap 50 done : time 5.778 sec Bootstrap 60 done : time 6.804 sec Bootstrap 70 done : time 7.851 sec Bootstrap 80 done : time 8.937 sec Bootstrap 90 done : time 9.979 sec Bootstrap 100 done : time 11.138 sec Bootstrap finished : total time 11.139 sec
こちらも11秒ほどで終了しました。計11.3秒とかなり速いです。前回の記事でMCMCpack::MCMCirt1dを用いて同様のデータで分析した際にburninが5000、mcmcが10000で設定したら大体55秒くらいかかってましたが、それと比べると中々の快挙ですね。とはいえ、EMは収束したらアルゴリズムを勝手に止めるという感じなので、そりゃ速いやろって感じですが。
結果
しっかり推定できているか確認します。信頼区間を導出する際には、バイアス補正をした形で行っていきます：
## Result ==================================================== # Bias correction ## Calculate bootstrapm mean boot_mean <- rowMeans(boot$theta) ## Bias (estimated mean - boot mean) bias <- model$parameters$theta - boot_mean ## 95% CI lwr <- apply(boot$theta, 1, quantile, probs = .025) + bias upr <- apply(boot$theta, 1, quantile, probs = .975) + bias ## Plot tibble(name = Senate$member, party = Senate$party, theta = model$parameters$theta, lwr = lwr, upr = upr) %>% mutate(party = if_else(party == 1, "Republican", "Democrat") %>% factor(levels = c("Republican", "Democrat"))) %>% ggplot(aes(x = theta, y = reorder(name, theta), color = party)) + geom_pointrange(aes(xmin = lwr, xmax = upr), size = 0.4) + xlab("Ideal Point") + theme_light() + theme(legend.title = element_blank(), axis.title.y = element_blank(), axis.text.y = element_text(size = 3), legend.position = "bottom", legend.direction = "horizontal")
赤は共和党で青は民主党を示します。党派性がくっきりとでた図になっていると思います。今までのベイズを使った推定値とほぼ同じ結果になっていると思います。前述の通り、試験問題解答データを使っても上手く推定できるかと思いますので、ぜひ活用してください。
おわりに
今回はPolya-Gamma data augmentationのスキームを用いたEMアルゴリズムによる項目反応理論モデルの推定を紹介しました。IRTモデルにはベイズ推定が用いられることが殆どですが、このようにEMアルゴリズムを用いた方が圧倒的に速いので割とオススメします。紹介した論文により詳細に手続きが記されているので興味がある人は見てみてください。私自身まだまだ勉強中ですので間違い等があれば指摘してください。ここまでご覧いただきありがとうございました。
再度にはなりますが、今回使用したコードはGithub上にまとめていますのでそちらもチェックしてみてください。
*1:Polson, N. G., Scott, J. G., & Windle, J. (2013). Bayesian inference for logistic models using Pólya–Gamma latent variables. Journal of the American statistical Association, 108(504), 1339-1349.
*2:項目反応理論を用いた政治学研究でもプロビットモデルが好まれています。
*3:Goplerud, M. (2019). A Multinomial Framework for Ideal Point Estimation. Political Analysis, 27(1), 69-89.
*4:Jiang, Z., & Templin, J. (2019). Gibbs samplers for logistic item response models via the Pólya–Gamma distribution: A computationally efficient data-augmentation strategy. psychometrika, 84(2), 358-374.
*5:Lewis, J. B., & Poole, K. T. (2004). Measuring bias and uncertainty in ideal point estimates via the parametric bootstrap. Political Analysis, 12(2), 105-127.
*6:詳しいことはこちら https://cran.r-project.org/web/packages/MCMCpack/MCMCpack.pdf
【R/Rcpp】Rcppを使って項目反応理論 (IRT) のスクラッチを高速化
タイトルの通り、Rcppで項目反応理論をスクラッチ実装しました。前回記事の追記で、ほぼすべての関数をC++で書き換えて高速化しました。
sunaninattahito.hatenablog.com
【追記: 2022/02/14】RcppAramdilloを使って行列計算をちゃんとしたところ、推定時間を半分以下に抑えられるようになりました。また、ヘッダーファイルを作成するなどして、コードファイルを分散させて整理しました。作成したコードや使い方などをGitHub上で公開してますので、より詳しくみたい方はそちらもチェックしてください。
おさらい
生成モデル ~ Metropolis-Hastings Algorithmまでザっとおさらいします。より詳しいことは前回の記事に載ってるのでそちらを参照してください。
個人 $i = 1,...,I$ が 問題 $j = 1,...,J$ にて正解する ($y_{ij} = 1$; otherwise 0) 確率を以下で与えます:
\begin{align*}
p_{ij} = \text{Pr}(y_{ij}=1\ |\ \alpha_j, \beta_j, \theta_i) = \text{logit}^{-1}(\beta_j \theta_i - \alpha_j).
\end{align*}
ここで、$\alpha_j$, $\beta_j$はそれぞれ問題$j$の難易度 (difficulty) と識別度 (discrimination)、$\theta_i$は個人$i$の能力 (ability) で、$\text{logit}^{-1}$は逆ロジット関数です。Likelihood $f(\cdot\ |\ \cdot)$は
\begin{align}
f(y\ |\ \alpha, \beta, \theta) &= \prod\limits_{i=1}^{I}\prod\limits_{j=1}^J \left[p_{ij}^{y_{ij}} (1-p_{ij})^{1 - y_{ij}}\right]\\
\end{align}
です。次に、各パラメータの事後分布を考えていきます。事前分布として、以下を与えます:
\begin{align*}
\alpha_j &\sim \mathcal{N}(a_0, A_0),\\
\beta_j &\sim \mathcal{N}(b_0, B_0), \\
\theta_i &\sim \mathcal{N}(0, 1).
\end{align*}
ベイズの定理より、その他のパラメータを所与としたうえでの各パラメータのconditionalな事後分布は、それぞれ以下で与えられます:
\begin{align*}
\pi(\alpha_j\ |\ y, \beta_j, \theta_i) &\propto f(y | \alpha, \beta, \theta)\pi(\alpha)\\
&\propto \prod\limits_{i=1}^{I} \left[p_{ij}^{y_{ij}} (1-p_{ij})^{1 - y_{ij}}\right] \cdot
N(\alpha_j \ |\ a_0, A_0) \forall j = 1,\dots J,\\
\pi(\beta_j\ |\ y, \alpha_j, \theta_i) &\propto f(y | \alpha, \beta, \theta)\pi(\beta)\\
&\propto \prod\limits_{i=1}^{I}\left[p_{ij}^{y_{ij}} (1-p_{ij})^{1 - y_{ij}}\right] \cdot
N(\beta_j \ |\ b_0, B_0) \forall j=1,...J,\\
\pi(\theta_i\ |\ y, \alpha_j, \beta_j) &\propto f(y | \alpha, \beta, \theta)\pi(\theta)\\
&\propto \prod\limits_{j=1}^J \left[p_{ij}^{y_{ij}} (1-p_{ij})^{1 - y_{ij}}\right] \cdot
N(\theta_i \ |\ 0, 1) \forall i=1,...,I.
\end{align*}
次に、Metropolis-Hastings Algorithmに必要なサンプルの採択確率等を説明します。ノテーションの簡略化のために任意のパラメータを$\delta_k$と定めます ($\delta_{1} = \alpha$, $\delta_2 = \beta$, $\delta_3 = \theta$)。まず、各パラメータの候補$\delta_k^*$を以下のようなランダムウォークな分布からサンプリングします。
\[\delta_k^* \sim N(\delta_k^{(t-1)}, \kappa_\delta)\]
$\delta_k^{(t-1)}$は1イテレーション前の$\delta_k$の値であり、$\kappa_\delta$はMH法でいうところのチューニングパラメータです。また、採択確率 (acceptance probability) は以下で計算します:
\[
ap = \min\left\{\frac{f\left(\delta_k^{*}\ | \ y, \delta_{-k}^{(t-1)}\right) g\left(\delta_k^{(t-1)}\ |\ \delta_k^{*} \right)}{f\left(\delta_k^{(t-1)}\ | \ y, \delta_{-k}^{(t-1)}\right) g\left(\delta_k^*\ |\ \delta_k^{(t-1)} \right)}, 1\right\}
\]
$g(\cdot |\ \cdot)$は提案分布です。また、とあるrandom number $u$を$U(0, 1)$からサンプリングして、$u < ap$ならばパラメータのサンプル候補である$\delta_k^{*}$を採択します。そうでない場合は、$\delta_k^{(t-1)}$をサンプルとして採択します。
上記の採択確率を対数に変換します。すなわち
\begin{align*}
\log ap = \min&\{\log f\left(\delta_k^{*}\ | \ y, \delta_{-k}^{(t-1)}\right) + \log g\left(\delta_k^{(t-1)}\ |\ \delta_k^{*} \right) \\
&- \left[\log f\left(\delta_k^{(t-1)}\ | \ y, \delta_{-k}^{(t-1)}\right) + \log\left(\delta_k^*\ |\ \delta_k^{(t-1)} \right)\right], 0\}
\end{align*}
であり、$\log(u) < \log(ap)$であれば$\delta_k^*$を採択します。そうでない場合は、$\delta_k^{(t-1)}$をサンプルとして採択します。これらのステップを任意のイテレーション数まで繰り返します。
Rcppでサンプラーを書く
すべてのパラメータのサンプリングに必要な関数などをirt_sampling.cppというファイルに一まとめにしました。
#include <Rcpp.h> using namespace Rcpp; // setseed function for replicability // [[Rcpp::export]] void set_seed(int seed) { Rcpp::Environment base_env("package:base"); Rcpp::Function ss = base_env["set.seed"]; ss(seed); } // Log-likelihood funcion // [[Rcpp::export]] NumericMatrix log_likelihood(NumericMatrix Y, NumericVector alpha, NumericVector beta, NumericVector theta) { int I = theta.length(); int J = alpha.length(); NumericMatrix prob(I, J); NumericMatrix log_p(I, J); for (int j = 0; j < J; j++) { for (int i = 0; i < I; i++) { prob(i, j) = std::exp(beta[j] * theta[i] - alpha[j]) / (1 + std::exp(beta[j] * theta[i] - alpha[j])); log_p(i, j) = Y(i, j) * std::log(prob(i, j)) + (1 - Y(i, j)) * std::log((1 - prob(i, j))); } } return(log_p); } // SAMPLING ALPHA // [[Rcpp::export]] NumericVector alpha_sampling(NumericMatrix Y, NumericVector alpha_old, NumericVector beta_old, NumericVector theta_old, double a0, double A0, double MH_alpha, int seed) { set_seed(seed); int J = Y.ncol(); // # of alpha NumericMatrix alpha_star_mat(J, 1); // candidate sample of alpha NumericMatrix log_prop_star_mat(J, 1); // candidate alpha proposal density (as matrix for convenience) NumericMatrix log_prop_old_mat(J, 1); // old alpha proposal density (as matrix) // Sampling from random-walk normal prior for (int j = 0; j < J; j++) { alpha_star_mat(j, _) = Rcpp::rnorm(1, alpha_old[j], MH_alpha); } // Convert into vector NumericVector alpha_star_vec = alpha_star_mat(_, 0); // Generate proposal density for (int j = 0; j < J; j++) { log_prop_star_mat(j, _) = Rcpp::dnorm(NumericVector::create(alpha_star_vec[j]), alpha_old[j], MH_alpha, true); log_prop_old_mat(j, _) = Rcpp::dnorm(NumericVector::create(alpha_old[j]), alpha_star_vec[j], MH_alpha, true); } // Convert into vector NumericVector log_prop_star_vec = log_prop_star_mat(_, 0); NumericVector log_prop_old_vec = log_prop_old_mat(_, 0); // Posterior density NumericVector log_cc_star = colSums(log_likelihood(Y, alpha_star_vec, beta_old, theta_old), true) + Rcpp::dnorm(alpha_star_vec, a0, A0, true); NumericVector log_cc_old = colSums(log_likelihood(Y, alpha_old, beta_old, theta_old), true) + Rcpp::dnorm(alpha_old, a0, A0, true); // Calculate acceptance probability NumericVector log_ap = pmin(log_cc_star + log_prop_old_vec - log_cc_old - log_prop_star_vec, 0); // Save samples (if log(u) < log(ap), accept alpha_star, otherwise alpha_old) NumericVector log_u = log(Rcpp::runif(J, 0, 1)); NumericVector sample(J); for (int j = 0; j < J; j++) { if (log_u[j] < log_ap[j]) { sample[j] = alpha_star_vec[j]; } else { sample[j] = alpha_old[j]; } } return(sample); } // SAMPLING BETA // [[Rcpp::export]] NumericVector beta_sampling(NumericMatrix Y, NumericVector alpha_old, NumericVector beta_old, NumericVector theta_old, double b0, double B0, double MH_beta, int seed) { set_seed(seed); int J = Y.ncol(); // # of beta NumericMatrix beta_star_mat(J, 1); // candidate of beta (as matrix for convenience) NumericMatrix log_prop_star_mat(J, 1); // candidate alpha proposal density (matrix) NumericMatrix log_prop_old_mat(J, 1); // old alpha proposal density (matrix) // Sampling from random-walk normal prior for (int j = 0; j < J; j++) { beta_star_mat(j, _) = Rcpp::rnorm(1, beta_old[j], MH_beta); } // Convert into vector NumericVector beta_star_vec = beta_star_mat(_, 0); // Generate proposal density for (int j = 0; j < J; j++) { log_prop_star_mat(j, _) = Rcpp::dnorm(NumericVector::create(beta_star_vec[j]), beta_old[j], MH_beta, true); log_prop_old_mat(j, _) = Rcpp::dnorm(NumericVector::create(beta_old[j]), beta_star_vec[j], MH_beta, true); } // Convert into vector NumericVector log_prop_star_vec = log_prop_star_mat(_, 0); NumericVector log_prop_old_vec = log_prop_old_mat(_, 0); // Calculate posterior density NumericVector log_cc_star = colSums(log_likelihood(Y, alpha_old, beta_star_vec, theta_old), true) + Rcpp::dnorm(beta_star_vec, b0, B0, true); NumericVector log_cc_old = colSums(log_likelihood(Y, alpha_old, beta_old, theta_old), true) + Rcpp::dnorm(beta_old, b0, B0, true); // Calculate acceptance probability NumericVector log_ap = pmin(log_cc_star + log_prop_old_vec - log_cc_old - log_prop_star_vec, 0); // Save samples (if log(u) < log(ap), accept alpha_star, otherwise alpha_old) NumericVector log_u = log(Rcpp::runif(J, 0, 1)); NumericVector sample(J); for (int j = 0; j < J; j++) { if (log_u[j] < log_ap[j]) { sample[j] = beta_star_vec[j]; } else { sample[j] = beta_old[j]; } } return(sample); } // SAMPLING THETA // [[Rcpp::export]] NumericVector theta_sampling(NumericMatrix Y, NumericVector alpha_old, NumericVector beta_old, NumericVector theta_old, double MH_theta, int seed) { set_seed(seed); int I = Y.nrow(); // # of theta NumericMatrix theta_star_mat(I, 1); // candidate sample for theta NumericMatrix log_prop_star_mat(I, 1); // candidate proposal density NumericMatrix log_prop_old_mat(I, 1); // old proposal density // Sampling from random-walk normal prior for (int i = 0; i < I; i++) { theta_star_mat(i, _) = Rcpp::rnorm(1, theta_old[i], MH_theta); } // Convert into vector NumericVector theta_star_vec = theta_star_mat(_, 0); // Generate proposal density for (int i = 0; i < I; i++) { log_prop_star_mat(i, _) = Rcpp::dnorm(NumericVector::create(theta_star_vec[i]), theta_old[i], MH_theta, true); log_prop_old_mat(i, _) = Rcpp::dnorm(NumericVector::create(theta_old[i]), theta_star_vec[i], MH_theta, true); } // Convert into vector NumericVector log_prop_star_vec = log_prop_star_mat(_, 0); NumericVector log_prop_old_vec = log_prop_old_mat(_, 0); // Calculate posterior density NumericVector log_cc_star = rowSums(log_likelihood(Y, alpha_old, beta_old, theta_star_vec), true) + Rcpp::dnorm(theta_star_vec, 0, 1, true); NumericVector log_cc_old = rowSums(log_likelihood(Y, alpha_old, beta_old, theta_old), true) + Rcpp::dnorm(theta_old, 0, 1, true); // Calculate acceptance probability NumericVector log_ap = pmin(log_cc_star + log_prop_old_vec - log_cc_old - log_prop_star_vec, 0); // Save samples (if log(u) < log(ap), accept alpha_star, otherwise alpha_old) NumericVector log_u = log(Rcpp::runif(I, 0, 1)); NumericVector sample(I); for (int i = 0; i < I; i++) { if (log_u[i] < log_ap[i]) { sample[i] = theta_star_vec[i]; } else { sample[i] = theta_old[i]; } } return(sample); } // MH SAMPLER // [[Rcpp::export]] List mh_sampler_irt(NumericMatrix datamatrix, NumericVector alpha, NumericVector beta, NumericVector theta, double a0 = 0, double A0 = 10, double b0 = 0, double B0 = 10, double MH_alpha = 0.3, double MH_beta = 0.3, double MH_theta = 0.3, int iter = 1000, int warmup = 1000, int thin = 1, int refresh = 100, int seed = 1) { int total_iter = iter + warmup; // total iteration int sample_iter = iter / thin; // # of samples to save NumericMatrix Y = datamatrix; // rename datamatrix to Y int I = Y.nrow(); // # of individuals int J = Y.ncol(); // # of items // rename NumericVector alpha_old = alpha; NumericVector beta_old = beta; NumericVector theta_old = theta; // create storages for parameters NumericMatrix theta_store(I, sample_iter); NumericMatrix alpha_store(J, sample_iter); NumericMatrix beta_store(J, sample_iter); // WARMUP Rcout << "Warmup: " << 1 << " / " << total_iter << " [ " << 0 << "% ]\n"; for (int g = 0; g < warmup; g++) { int seed2 = seed + g; if ((g + 1) % refresh == 0) { double gg = g + 1; double ti2 = total_iter; double per = std::round((gg / ti2) * 100); Rcout << "Warmup: " << (g + 1) << " / " << total_iter << " [ " << per << "% ]\n"; } theta = theta_sampling(Y, alpha_old, beta_old, theta_old, MH_theta, seed2); theta_old = theta; alpha = alpha_sampling(Y, alpha_old, beta_old, theta_old, a0, A0, MH_alpha, seed2); alpha_old = alpha; beta = beta_sampling(Y, alpha_old, beta_old, theta_old, b0, B0, MH_beta, seed2); beta_old = beta; } // SAMPLING double gg = warmup + 1; double ti2 = total_iter; double per = std::round((gg / ti2) * 100); Rcout << "Sampling: " << gg << " / " << total_iter << " [ " << per << "% ]\n"; for (int g = warmup; g < total_iter; g++) { int seed2 = seed + g; if ((g + 1) % refresh == 0) { double gg = g + 1; double ti2 = total_iter; double per = std::round((gg / ti2) * 100); Rcout << "Sampling: " << (g + 1) << " / " << total_iter << " [ " << per << " % ]\n"; } theta = theta_sampling(Y, alpha_old, beta_old, theta_old, MH_theta, seed2); theta_old = theta; alpha = alpha_sampling(Y, alpha_old, beta_old, theta_old, a0, A0, MH_alpha, seed2); alpha_old = alpha; beta = beta_sampling(Y, alpha_old, beta_old, theta_old, b0, B0, MH_beta, seed2); beta_old = beta; if (g % thin == 0) { double th = thin; double wu = warmup; double gg = g; double ggg = (g - warmup) / thin; // Reparameterization (fix theta with mean 0 and sd 1) NumericVector theta_std = (theta_old - mean(theta_old)) / sd(theta_old); NumericVector alpha_std = beta_old * mean(theta_old) - alpha_old; NumericVector beta_std = beta_old * sd(theta_old); theta_store(_, ggg) = theta_std; alpha_store(_, ggg) = alpha_std; beta_store(_, ggg) = beta_std; } } List L = List::create(Named("alpha") = alpha_store, Named("beta") = beta_store, Named("theta") = theta_store); return(L); }
このコードの中には6つの関数があり、以下がそれぞれの説明です。
set_seed: 再現性確保のためにRからset.seed関数を持ってきて、C++内で使用できるようにする関数log_likelihood: 対数尤度を計算する関数alpha_sampling: $\alpha$をサンプリングする関数beta_sampling: $\beta$をサンプリングする関数theta_sampling: $\theta$をサンプリングする関数mh_sampler_irt: MCMCを回す関数
また、{MCMCpack}パッケージにあるMCMCirt1d関数においては、パラメータのreparameterizationが行われており、$\theta_i$の標準化 (mean = 0, sd = 1)、またそれに付随する項目パラメータの変換が為されています。今回の自作関数でも同様の計算を施します。Reparameterization後のパラメータをそれぞれ$\alpha_j^{adj}$, $\beta_j^{adj}$, $\theta_{i}^{adj}$とすると
\begin{align*}
\theta_i^{adj} &= \frac{\theta_i - \overline{\theta}}{s_\theta}\\
\beta_j^{adj} &= \beta_j s_\theta\\
\alpha_j^{adj} &= \beta_j \overline{\theta} - \alpha_j
\end{align*}
が得られます。また、先ほどの関数たちをRで使用するためにコンパイルします。
library(Rcpp) sourceCpp("cpp/irt_sampling.cpp")
さらに、事後分布の処理や諸々の利便化のために、下記のirt_cpp関数を定義します。
irt_cpp <- function(datamatrix, iter, warmup, thin, refresh, seed, init, tuning_par, prior) { cat("\n================================================================\n") cat("Run Metropolis-Hasting Sampler for 2PL item response model...\n\n") cat(" Observations:", nrow(datamatrix) * ncol(datamatrix),"\n") cat(" Number of individuals:", nrow(datamatrix), "\n") cat(" Number of items:", ncol(datamatrix), "\n") cat(" Total correct response:", sum(as.numeric(datamatrix), na.rm = TRUE), "/", nrow(datamatrix) * ncol(datamatrix), "[", round(sum(as.numeric(datamatrix), na.rm = TRUE) / (nrow(datamatrix) * ncol(datamatrix)), 2) * 100, "%]","\n\n") cat(" Priors: \n") cat(" alpha ~", paste0("N(", prior$a0, ", ", prior$A0, "),"), "beta ~", paste0("N(", prior$b0, ", ", prior$B0, "),"), "theta ~ N(0, 1).\n") cat("================================================================\n\n") # Preparation ## Measure starting time stime <- proc.time()[3] ## Set seed set.seed(seed) # Run sampler mcmc <- mh_sampler_irt(datamatrix = Y, alpha = init$alpha, beta = init$beta, theta = init$theta, a0 = prior$a0, A0 = prior$A0, b0 = prior$b0, B0 = prior$B0, MH_alpha = tuning_par$alpha, MH_beta = tuning_par$beta, MH_theta = tuning_par$theta, iter = iter, warmup = warmup, thin = thin, refresh = refresh) # Generate variable labels label_iter <- paste0("iter_", 1:(iter/thin)) alpha_lab <- paste0("alpha_", colnames(datamatrix)) beta_lab <- paste0("beta_", colnames(datamatrix)) theta_lab <- paste0("theta_", rownames(datamatrix)) colnames(mcmc$alpha) <- colnames(mcmc$beta) <- colnames(mcmc$theta) <- label_iter rownames(mcmc$alpha) <- alpha_lab rownames(mcmc$beta) <- beta_lab rownames(mcmc$theta) <- theta_lab # Redefine quantile function lwr <- function(x) quantile(x, probs = 0.025, na.rm = TRUE) upr <- function(x) quantile(x, probs = 0.975, na.rm = TRUE) mean_ <- function(x) mean(x, na.rm = TRUE) median_ <- function(x) median(x, na.rm = TRUE) # Calculate statistics alpha_post <- data.frame(parameter = alpha_lab, mean = apply(mcmc$alpha, 1, mean_), median = apply(mcmc$alpha, 1, median_), lwr = apply(mcmc$alpha, 1, lwr), upr = apply(mcmc$alpha, 1, upr)) beta_post <- data.frame(parameter = beta_lab, mean = apply(mcmc$beta, 1, mean_), median = apply(mcmc$beta, 1, median_), lwr = apply(mcmc$beta, 1, lwr), upr = apply(mcmc$beta, 1, upr)) theta_post <- data.frame(parameter = theta_lab, mean = apply(mcmc$theta, 1, mean_), median = apply(mcmc$theta, 1, median_), lwr = apply(mcmc$theta, 1, lwr), upr = apply(mcmc$theta, 1, upr)) # Aggregate result <- list(summary = list(alpha = alpha_post, beta = beta_post, theta = theta_post), sample = list(alpha = mcmc$alpha, beta = mcmc$beta, theta = mcmc$theta)) etime <- proc.time()[3] cat(crayon::yellow("Done: Total time", round(etime - stime, 1), "sec\n")) return(result) }
応用：アメリカ連邦議会上院議員の理想点推定
前回はUS Supreme Courtの判決データを使って各判事の理想点推定をしましたが、今回は{MCMCpack}パッケージに収録されているアメリカ連邦議会上院の第106議会での点呼式投票データ*1を使って各議員の理想点推定をしていこうと思います。
まずは、データを読み込みましょう。
data(Senate, package = "MCMCpack")
データを確認すると、点呼式投票 (rc~列) 以外の議員に関するデータが含まれていることがわかります。
Senate[1:10, 1:10]
id statecode state party member rc1 rc2 rc3 rc4 rc5 SESSIONS 49700 41 ALABAMA 1 SESSIONS 1 0 0 0 1 SHELBY 94659 41 ALABAMA 1 SHELBY 1 0 0 0 1 MURKOWSKI 14907 81 ALASKA 1 MURKOWSKI 1 0 0 0 1 STEVENS 12109 81 ALASKA 1 STEVENS 1 0 0 0 1 KYL 15429 61 ARIZONA 1 KYL 1 0 0 0 1 MCCAIN 15039 61 ARIZONA 1 MCCAIN 1 0 0 0 1 HUTCHINSON 29306 42 ARKANSA 1 HUTCHINSON 1 0 0 0 1 LINCOLN 29305 42 ARKANSA 0 LINCOLN 1 0 0 1 0 BOXER 15011 71 CALIFOR 0 BOXER 1 1 1 1 0 FEINSTEIN 49300 71 CALIFOR 0 FEINSTEIN 1 1 1 1 0
行名は議員の名前になっており、属する州や政党のインデックス (1 = Republican, 0 = Democrat)が入ってます。とはいえ、IRTをするうえでは不要なので全部切り捨てて、またSenateデータはデータフレームなので行列に変換します。
Y <- as.matrix(Senate[, 6:length(Senate)])
次に、初期値や事前分布、MH法のチューニングパラメータを定義します。今回も項目パラメータの事前分布を$\alpha_j\sim N(0, 10)$, $\beta_j\sim N(1, 0.2)$と定めます。
# Initial values init <- list(alpha = alpha_init, beta = beta_init, theta = theta_init) # Tuning parameters tuning_par <- list(alpha = 2, beta = 0.6, theta = 0.9) # Priors prior <- list(a0 = 0, # mean for alpha A0 = 10, # sd for alpha b0 = 1, # mean for beta B0 = 0.2) # sd for beta
これらを全て先ほど定義したirt_cpp関数にぶち込んで、IRTをしていきます。
fit <- irt_cpp(datamatrix = Y, iter = 5000, warmup = 3000, thin = 5, refresh = 500, seed = 1, init = init, tuning_par = tuning_par, prior = prior)
================================================================ Run Metropolis-Hasting Sampler for 2PL item response model... Observations: 68544 Number of individuals: 102 Number of items: 672 Total correct response: 42458 / 68544 [ 62 %] Priors: alpha ~ N(0, 10), beta ~ N(1, 0.2), theta ~ N(0, 1). ================================================================ Warmup: 1 / 8000 [ 0% ] Warmup: 500 / 8000 [ 6% ] Warmup: 1000 / 8000 [ 13% ] Warmup: 1500 / 8000 [ 19% ] Warmup: 2000 / 8000 [ 25% ] Warmup: 2500 / 8000 [ 31% ] Warmup: 3000 / 8000 [ 38% ] Sampling: 3001 / 8000 [ 38% ] Sampling: 3500 / 8000 [ 44 % ] Sampling: 4000 / 8000 [ 50 % ] Sampling: 4500 / 8000 [ 56 % ] Sampling: 5000 / 8000 [ 63 % ] Sampling: 5500 / 8000 [ 69 % ] Sampling: 6000 / 8000 [ 75 % ] Sampling: 6500 / 8000 [ 81 % ] Sampling: 7000 / 8000 [ 88 % ] Sampling: 7500 / 8000 [ 94 % ] Sampling: 8000 / 8000 [ 100 % ] Done: Total time 369.8 sec
６分ほどで終わりましたが、高速化したのにもかかわらずまだちょっと遅めですね。後程、MCMCpack::MCMCirt1d関数とスピードを比べてみようと思います。ちなみに前回のRベースの関数での実行時間は約8分50秒でした。２分半強ぐらい高速化できました。
結果を確認しましょう。結果はfit$summary$で抜け出せるようにしています。
library(tidyverse) # Extract the result theta <- fit$summary$theta %>% mutate(name = rownames(Y), # Add senators' name party = Senate$party) # Add senators' party # Plot theta %>% ggplot(aes(y = reorder(name, mean), x = mean, color = factor(party))) + geom_pointrange(aes(xmin = lwr, xmax = upr)) + theme_light() + xlab("Estimated Ideal Point") + ylab("") + ggtitle("106th US Senate Roll-Call Vote") + scale_color_discrete(limits = c("1", "0"), label = c("Republican", "Democrat")) + theme(legend.position = "bottom", legend.direction = "horizontal", legend.title = element_blank())
所属党ごとの政策選好の違いがくっきりと見て取れます。ちゃんと推定できているか不安なので、MCMCpack::MCMCirt1d関数で確認してみます。また、せっかくなので実行時間も測ってみます。
# Measure running time stime <- proc.time()[3] # Run mcmc_fit <- MCMCpack::MCMCirt1d(Y, burnin = 3000, mcmc = 5000, thin = 5, seed = 1, verbose = 1000) etime <- proc.time()[3] # Output running time etime - stime
elapsed
55.228
いや、速すぎね？？？？？？こっちもCpp使ってるんですけど？？？？？まずは結果を確認します。
theta_mcmcp <- summary(mcmc_fit)$quantiles %>% as_tibble() %>% mutate(name = rownames(Y), party = Senate$party, mean = `50%`, lwr = `2.5%`, upr = `97.5%`) %>% select(name:upr) theta_mcmcp %>% ggplot(aes(y = reorder(name, mean), x = mean, color = factor(party))) + geom_pointrange(aes(xmin = lwr, xmax = upr)) + theme_light() + xlab("Estimated Ideal Point") + ylab("") + ggtitle("106th US Senate Roll-Call Vote: Estimated with MCMCpack") + scale_color_discrete(limits = c("1", "0"), label = c("Republican", "Democrat")) + theme(legend.position = "bottom", legend.direction = "horizontal", legend.title = element_blank(), axis.text.y = element_text(size = 4))
符号が自作関数と反転してますが、大体同じような結果ではないでしょうか。符号反転の問題は後からどうにでもできることなのでどうでもいいです。いやー、しかし{MCMCpack}速すぎ問題ありますよね。どうすればあそこまで速くなるんだろう…
おわりに
今回やってわかったことはMCMCpack速すぎじゃね～～～～～？？？？？？？？？ということでした。RcppArmadilloなどのLinear Algebra系のやつも使いこなせるようになればもっと速くできるのでしょうか。精進していこうと思います。
【R/Rcpp】項目反応理論 (IRT) をスクラッチで実装する
タイトル通りです。IRTをスクラッチでMCMC実装しました。検索をかけてもあまり実例が出てこなかったため、自分のメモ帳替わりということも含めて記事にします。
本記事では、Wim J. van der Linden (2016) の``Handbook of Item Response Theory Volume 2: Statistical Tools" 15章を参考にしていますので、より詳しく知りたい方はそちらをご覧ください。
また、当方も勉強中のため間違っているところが多々あると思うので、その都度お知らせいただけると幸いです。
準備
ざっくり書いていきます。個人 $i = 1,...,I$ が 問題 $j = 1,...,J$ にて正解する ($y_{ij} = 1$; otherwise 0) 確率を以下で与えます:
\begin{align*}
p_{ij} = \text{Pr}(y_{ij}=1\ |\ \alpha_j, \beta_j, \theta_i) = \text{logit}^{-1}(\beta_j \theta_i - \alpha_j).
\end{align*}
ここで、$\alpha_j$, $\beta_j$はそれぞれ問題$j$の難易度 (difficulty) と識別度 (discrimination)、$\theta_i$は個人$i$の能力 (ability) で、$\text{logit}^{-1}$は逆ロジット関数です。Likelihood $f(\cdot\ |\ \cdot)$は
\begin{align}
f(y\ |\ \alpha, \beta, \theta) &= \prod\limits_{i=1}^{I}\prod\limits_{j=1}^J \left[p_{ij}^{y_{ij}} (1-p_{ij})^{1 - y_{ij}}\right]\\
\end{align}
です。次に、各パラメータの事後分布を考えていきます。事前分布として、以下を与えます:
\begin{align*}
\alpha_j &\sim \mathcal{N}(a_0, A_0),\\
\beta_j &\sim \mathcal{N}(b_0, B_0), \\
\theta_i &\sim \mathcal{N}(0, 1).
\end{align*}
ベイズの定理より、その他のパラメータを所与としたうえでの各パラメータのconditionalな事後分布は、それぞれ以下で与えられます:
\begin{align*}
\pi(\alpha_j\ |\ y, \beta_j, \theta_i) &\propto f(y | \alpha, \beta, \theta)\pi(\alpha)\\
&\propto \prod\limits_{i=1}^{I} \left[p_{ij}^{y_{ij}} (1-p_{ij})^{1 - y_{ij}}\right] \cdot
N(\alpha_j \ |\ a_0, A_0) \forall j = 1,\dots J,\\
\pi(\beta_j\ |\ y, \alpha_j, \theta_i) &\propto f(y | \alpha, \beta, \theta)\pi(\beta)\\
&\propto \prod\limits_{i=1}^{I}\left[p_{ij}^{y_{ij}} (1-p_{ij})^{1 - y_{ij}}\right] \cdot
N(\beta_j \ |\ b_0, B_0) \forall j=1,...J,\\
\pi(\theta_i\ |\ y, \alpha_j, \beta_j) &\propto f(y | \alpha, \beta, \theta)\pi(\theta)\\
&\propto \prod\limits_{j=1}^J \left[p_{ij}^{y_{ij}} (1-p_{ij})^{1 - y_{ij}}\right] \cdot
N(\theta_i \ |\ 0, 1) \forall i=1,...,I.
\end{align*}
超ざっくり要点だけさらっていきましたが、こんな感じです。あとはサンプラーを作るだけです。
MCMCする (Metropolis-Hastings Algorithm)
通常のギブスサンプリングだと上記の目標分布からのサンプリングは困難ということで、Metropolis-Hastings Algorithmを用います。
ここで、ノテーションの簡略化のために任意のパラメータを$\delta_k$と定めます ($\delta_{1} = \alpha$, $\delta_2 = \beta$, $\delta_3 = \theta$)。まず、各パラメータの候補$\delta_k^*$を以下のようなランダムウォークな分布からサンプリングします。
\[\delta_k^* \sim N(\delta_k^{(t-1)}, \kappa_\delta)\]
$\delta_k^{(t-1)}$は1イテレーション前の$\delta_k$の値であり、$\kappa_\delta$はMH法でいうところのチューニングパラメータです。また、採択確率 (acceptance probability) は以下で計算します:
\[
ap = \min\left\{\frac{f\left(\delta_k^{*}\ | \ y, \delta_{-k}^{(t-1)}\right) g\left(\delta_k^{(t-1)}\ |\ \delta_k^{*} \right)}{f\left(\delta_k^{(t-1)}\ | \ y, \delta_{-k}^{(t-1)}\right) g\left(\delta_k^*\ |\ \delta_k^{(t-1)} \right)}, 1\right\}
\]
$g(\cdot |\ \cdot)$は提案分布です。また、とあるrandom number $u$を$U(0, 1)$からサンプリングして、$u < ap$ならばパラメータのサンプル候補である$\delta_k^{*}$を採択します。そうでない場合は、$\delta_k^{(t-1)}$をサンプルとして採択します。
しかし、コンピューター的な問題で$ap$等の確率の値がPCが認識できないレベルまで小さくなる場合があります (例えば、1000個の観測とそれぞれの確率が0.001の場合、つまり0.0011000の場合を想像してみてください)。そこで、上記の採択確率を対数に変換します。すなわち
\begin{align*}
\log ap = \min&\{\log f\left(\delta_k^{*}\ | \ y, \delta_{-k}^{(t-1)}\right) + \log g\left(\delta_k^{(t-1)}\ |\ \delta_k^{*} \right) \\
&- \left[\log f\left(\delta_k^{(t-1)}\ | \ y, \delta_{-k}^{(t-1)}\right) + \log\left(\delta_k^*\ |\ \delta_k^{(t-1)} \right)\right], 0\}
\end{align*}
であり、$\log(u) < \log(ap)$であれば$\delta_k^*$を採択します。そうでない場合は、$\delta_k^{(t-1)}$をサンプルとして採択します。これらのステップを任意のイテレーション数まで繰り返します。
サンプラーを作る
以下でサンプリングのための関数を定義していきます。また、高速化のためにC++で一部関数を書きました。
対数尤度を計算する関数
この関数では対数尤度を計算します。各パラメータのサンプリングの際に対数尤度を用いるので補助的に定義します。また、forループを使用するのでC++で書きました。ファイル名はlog_likelihood.cppです。
//log_likelihood.cpp #include <Rcpp.h> using namespace Rcpp; // [[Rcpp::export]] NumericMatrix log_likelihood(NumericMatrix Y, NumericVector alpha, NumericVector beta, NumericVector theta) { int I = theta.length(); int J = alpha.length(); NumericMatrix prob(I, J); NumericMatrix log_p(I, J); for (int j = 0; j < J; j++) { for (int i = 0; i < I; i++) { prob(i, j) = std::exp(beta[j] * theta[i] - alpha[j]) / (1 + std::exp(beta[j] * theta[i] - alpha[j])); log_p(i, j) = Y(i, j) * std::log(prob(i, j)) + (1 - Y(i, j)) * std::log((1 - prob(i, j))); } } return(log_p); }
また、この関数を利用するために{Rcpp}パッケージを読み込んで、コンパイルしましょう。そうすればlog_likelihood関数として利用できます。
library(Rcpp) sourceCpp("log_likelihood.cpp")
$\alpha$をサンプリングする関数
alpha_samplingという関数を定義します。
alpha_sampling <- function(Y, old_data, a0, A0) { # sum function with na.rm=TRUE sum_ <- function(x) sum(x, na.rm = TRUE) # Get old parameter alpha_old <- old_data$alpha MH_alpha <- old_data$MH$alpha J <- length(alpha_old) # Generate candidate parameter: alpha_can ~ N(alpha_old, tuning_param_alpha) alpha_star <- suppressWarnings(rnorm(J, alpha_old, MH_alpha)) # Calculate acceptance probability ## Log posterior density ### Candidate: log(f(Y | theta_old, alpha_star, beta_old)) + log(pi(N(alpha_star | a0, A0))) log_cc_star <- apply(log_likelihood(Y, alpha = alpha_star, beta = old_data$beta, theta = old_data$theta), 2, sum_) + log(dnorm(alpha_star, a0, A0)) ### Old: log(f(Y | theta_old, alpha_old, beta_old)) + log(pi(N(alpha_old | a0, A0))) log_cc_old <- apply(log_likelihood(Y, alpha_old, old_data$beta, old_data$theta), 2, sum_) + log(dnorm(alpha_old, a0, A0)) ## Proposal density ### Candidate: g_m(alpha_star | alpha_old) log_prop_star <- log(dnorm(alpha_star, alpha_old, MH_alpha)) ### Old: # g_m(alpha_old | alpha_star) log_prop_old <- log(dnorm(alpha_old, alpha_star, MH_alpha)) ## Acceptance probability log_ac <- pmin(log_cc_star + log_prop_old - log_cc_old - log_prop_star, 0) ## Acceptance indicator - if log(u) < log(acceptance prob), then return 1 (otherwise 0) acc_new <- ifelse(log(runif(J)) < log_ac, 1, 0) # Save current_data <- old_data ## If acceptance indicator == 1, accept alpha_star current_data$alpha <- ifelse(acc_new == 1, alpha_star, alpha_old) ## Calculate acceptance rate current_data$acc$alpha_acc <- current_data$acc$alpha_acc + acc_new return(current_data) }
$\beta$をサンプリングする関数
同様に、beta_samplingという関数を定義します。
beta_sampling <- function(Y, old_data, b0, B0) { sum_ <- function(x) sum(x, na.rm = TRUE) # Get old parameter beta_old <- old_data$beta MH_beta <- old_data$MH$beta J <- length(beta_old) # Generate candidate parameter: beta_can ~ N(ln beta_old, tuning_param_beta) beta_star <- suppressWarnings(rnorm(J, beta_old, MH_beta)) # Calculate acceptance probability ## Log posterior density ### Candidate: log(f(Y | theta_old, alpha_old, beta_star)) + log(pi(N(beta_star | b0, B0))) log_cc_star <- apply(log_likelihood(Y, alpha = old_data$alpha, beta = beta_star, theta = old_data$theta), 2, sum_) + log(dnorm(beta_star, b0, B0)) ### Old: log(f(Y | theta_old, alpha_old, beta_old)) + log(pi(N(beta_old | b0, B0))) log_cc_old <- apply(log_likelihood(Y, alpha = old_data$alpha, beta = beta_old, theta = old_data$theta), 2, sum_) + log(dnorm(beta_old, b0, B0)) ## Proposal density ### Candidate: g_m(beta_star | beta_old) log_prop_star <- log(dnorm(beta_star, beta_old, MH_beta)) ### Old: # g_m(beta_old | beta_star) log_prop_old <- log(dnorm(beta_old, beta_star, MH_beta)) ## Acceptance probability log_ac <- pmin(log_cc_star + log_prop_old - log_cc_old - log_prop_star, 0) ## Acceptance indicator - if log(u) < log(acceptance prob), then return 1 (otherwise 0) acc_new <- ifelse(log(runif(J)) < log_ac, 1, 0) # Save current_data <- old_data ## If acceptance indicator == 1, accept beta_star current_data$beta <- ifelse(acc_new == 1, beta_star, beta_old) ## Calculate acceptance rate current_data$acc$beta_acc <- old_data$acc$beta_acc + acc_new return(current_data) }
$\theta$をサンプリングする関数
theta_samplingという関数を定義します。パラメータのサンプリング関数はそれぞれ事前分布の部分を書き換えただけで、そこまで難しくはないと思います。
theta_sampling <- function(Y, old_data) { sum_ <- function(x) sum(x, na.rm = TRUE) # Get old parameter theta_old <- old_data$theta MH_theta <- old_data$MH$theta I <- length(theta_old) # Generate candidate parameter: theta_can ~ N(theta_old, tuning_param_theta) theta_star <- suppressWarnings(rnorm(I, theta_old, MH_theta)) # Calculate acceptance probability ## Log posterior density ### Candidate: log(f(Y | theta_star, alpha_old, beta_old)) + log(pi(N(theta_star | 0, 1))) log_cc_star <- apply(log_likelihood(Y, alpha = old_data$alpha, beta = old_data$beta, theta = theta_star), 1, sum_) + log(dnorm(theta_star, 0, 1)) ### Old: log(f(Y | theta_old, alpha_old, beta_old)) + log(pi(N(theta_old | 0, 1))) log_cc_old <- apply(log_likelihood(Y, alpha = old_data$alpha, beta = old_data$beta, theta = theta_old), 1, sum_) + log(dnorm(theta_old, 0, 1)) ## Proposal density ### Candidate: g_m(theta_star | theta_old) log_prop_star <- log(dnorm(theta_star, mean = theta_old, sd = MH_theta)) ### Old: # g_m(theta_old | theta_star) log_prop_old <- log(dnorm(theta_old, mean = theta_star, sd = MH_theta)) ## Acceptance probability log_ac <- pmin(log_cc_star + log_prop_old - log_cc_old - log_prop_star, 0) ## Acceptance indicator - if log(u) < log(acceptance prob), then return 1 (otherwise 0) acc_new <- ifelse(log(runif(I)) < log_ac, 1, 0) # Save current_data <- old_data ## If acceptance indicator == 1, accept theta_star current_data$theta <- ifelse(acc_new == 1, theta_star, theta_old) ## Calculate acceptance rate current_data$acc$theta_acc <- old_data$acc$theta_acc + acc_new return(current_data) }
MHサンプラー
最後にMH法によるサンプラーMH_irtを定義します。R映えというかサンプリング状況を見やすくするために、イテレーション数の出力など色々加えてます。また、サンプリングの順番は$\theta\rightarrow\alpha\rightarrow\beta$です。
MH_irt <- function(datamatrix, alpha_init = NULL, beta_init = NULL, theta_init = NULL, MH_alpha = 0.4, MH_beta = 0.4, MH_theta = 0.4, iter = 2000, warmup = 1000, thin = 1, refresh = 100, seed = NULL, a0 = 1, A0 = 10, b0 = 0, B0 = 10) { # Rename matrix as Y for convenience Y <- datamatrix # Extract the # of individuals and items I <- nrow(Y) J <- ncol(Y) cat("\n================================================================\n") cat("Run Metropolis-Hasting Sampler for 2PL Item response model...\n\n") cat(" Observations:", I * J,"\n") cat(" Number of individuals:", I, "\n") cat(" Number of items:", J, "\n") cat(" Total correct response:", sum(as.numeric(Y), na.rm = TRUE), "/", I * J, "[", round(sum(as.numeric(Y), na.rm = TRUE) / (I * J), 2) * 100, "%]","\n\n") cat(" Priors: \n") cat(" alpha ~", paste0("N(", a0, ", ", A0, "),"), "beta ~", paste0("N(", b0, ", ", B0, "),"), "theta ~ N(0, 1).\n") cat("================================================================\n\n") # Preparation ## Measure starting time stime <- proc.time()[3] ## Set seed if (is.null(seed)) { seed <- as.integer(runif(1, 1, 50000)) } set.seed(seed) ## Define the number of iterations total_iter <- iter + warmup ## Generate storage alpha_store <- matrix(NA, J, iter/thin) beta_store <- matrix(NA, J, iter/thin) theta_store <- matrix(NA, I, iter/thin) ## Define initial number if (is.null(alpha_init)) { alpha_init <- rep(0, J) } if (is.null(beta_init)) { beta_init <- rep(1, J) } if (is.null(theta_init)) { theta_init <- rep(0.1, I) } ## Generate data current_data <- list(alpha = alpha_init, beta = beta_init, theta = theta_init, MH = list(alpha = MH_alpha, beta = MH_beta, theta = MH_theta), acc = list(alpha_acc = 0, beta_acc = 0, theta_acc = 0)) ## Generate priors priors <- list(a0 = a0, A0 = A0, b0 = b0, B0 = B0) # SAMPLING PHASE for (ii in 1:total_iter) { # Sampling theta parameter current_data <- theta_sampling(Y, current_data) if (all(is.na(current_data$theta))) { cat("Error at", ii, ": All values are NAs.\n") break } # Sampling alpha parameter current_data <- alpha_sampling(Y, current_data, priors$a0, priors$A0) if (all(is.na(current_data$alpha))) { cat("Error at", ii, ": All values are NAs.\n") break } # Sampling beta parameter current_data <- beta_sampling(Y, current_data, priors$b0, priors$B0) if (all(is.na(current_data$beta))) { cat("Error at", ii, ": All values are NAs.\n") break } if (ii <= warmup & ii %% refresh == 0) { cat("Warmup:", ii, "/", total_iter, "[", round(ii/total_iter, 2) * 100, "%]", round(proc.time()[3] - stime, 1), "sec\n") } if (ii > warmup) { if ((ii - warmup) %% thin == 0) { iii <- (ii - warmup) / thin alpha_store[, iii] <- current_data$alpha beta_store[, iii] <- current_data$beta theta_store[, iii] <- current_data$theta } if (ii %% refresh == 0) { cat("Sampling:", ii, "/", total_iter, "[", round(ii/total_iter, 2) * 100, "%]", round(proc.time()[3] - stime, 1), "sec\n") } } } # Calculate acceptance rate alpha_acc <- current_data$acc$alpha_acc / total_iter beta_acc <- current_data$acc$beta_acc / total_iter theta_acc <- current_data$acc$theta_acc / total_iter # Generate variable labels label_iter <- paste0("iter_", 1:(iter/thin)) alpha_lab <- paste0("alpha_", 1:J) beta_lab <- paste0("beta_", 1:J) theta_lab <- paste0("theta_", 1:I) colnames(alpha_store) <- colnames(beta_store) <- colnames(theta_store) <- label_iter rownames(alpha_store) <- alpha_lab rownames(beta_store) <- beta_lab rownames(theta_store) <- theta_lab # Redefine quantile function lwr <- function(x) quantile(x, probs = 0.025, na.rm = TRUE) upr <- function(x) quantile(x, probs = 0.975, na.rm = TRUE) mean_ <- function(x) mean(x, na.rm = TRUE) median_ <- function(x) median(x, na.rm = TRUE) # Calculate statistics alpha_post <- data.frame(variable = alpha_lab, mean = apply(alpha_store, 1, mean_), median = apply(alpha_store, 1, median_), lwr = apply(alpha_store, 1, lwr), upr = apply(alpha_store, 1, upr)) beta_post <- data.frame(variable = beta_lab, mean = apply(beta_store, 1, mean_), median = apply(beta_store, 1, median_), lwr = apply(beta_store, 1, lwr), upr = apply(beta_store, 1, upr)) theta_post <- data.frame(variable = theta_lab, mean = apply(theta_store, 1, mean_), median = apply(theta_store, 1, median_), lwr = apply(theta_store, 1, lwr), upr = apply(theta_store, 1, upr)) # Aggregate result <- list(summary = list(alpha = alpha_post, beta = beta_post, theta = theta_post), sample = list(alpha = alpha_store, beta = beta_store, theta = theta_store), ac_rate = list(alpha = alpha_acc, beta = beta_acc, theta = theta_acc)) etime <- proc.time()[3] cat(crayon::yellow("Done: Total time", round(etime - stime, 1), "sec\n")) return(result) }
さあ、準備は整いました。実際に動かしてみましょう。
応用：アメリカ最高裁判事の理想点推定
政治学では、議会における点呼式投票や裁判所における審判記録などを用いて各アクターの理想点 (ideal point) を推定します。理想点とは簡単に言えば「イデオロギー」のようなものであり、例えばリベラル・保守のようなものです。IRTは理想点推定に頻繁に用いられるテクニックであり、Clinton, Jackman and Rivers (2004)*1で詳しく説明されています。
一次元の政策空間$R$上に政治アクター$i=1,...,I$がいるとして、点呼式投票 or 判決 $j=1,...,J$について賛成票 (Yea) を投じる場合は$y_{ij}=1$となり、反対票 (Nay) を投じる場合は$y_{ij}=0$となります。ここで、棄権や欠席は欠損値とします*2。この時、賛成票を投じる確率は先ほどのIRTの式で表されます*3
\begin{align*}
\text{Pr}(y_{ij}=1\ |\ \alpha_j, \beta_j, \theta_i) = \text{logit}^{-1}(\beta_j \theta_i - \alpha_j).
\end{align*}
ここで、$\alpha_j, \beta_j$はそれぞれ政策争点のcutpoint (cutpointを超える$\theta$を持つ$i$は投票する)、分極度 (polarity, saliency) として捉えられます。また、$\theta_i$が$i$の理想点です。
先ほども述べましたが、アメリカ最高裁判事の理想点が推定されている研究は多々あります。どの判事がリベラルで保守なのか等様々に議論されています。また、皆さん大好き{MCMCpack}の作者であるMartinさんとQuinnさんもその一例です。(Martin & Quinn 2002)*4。
嬉しいことに、{MCMCpack}には2000年期の全会一致の判決以外の判決43個と判事9人を記録したデータが提供されています。今回はそれを利用します。
data(SupremeCourt, package = "MCMCpack") Y <- t(SupremeCourt) Y[1:9, 1:5]
1 2 3 4 5 Rehnquist 0 0 0 0 1 Stevens 1 1 1 0 1 O Connor 1 0 0 0 0 Scalia 0 0 0 0 0 Kennedy 1 0 0 0 1 Souter 1 1 1 0 0 Thomas 0 0 0 0 0 Ginsburg 1 1 1 0 0 Breyer 1 1 1 1 0
上記のように、点呼式投票データや判決データは教育学や心理学でいうテストデータと同じ構造になっていることがわかります。それでは早速MCMCしましょう。今回は$\alpha_j$の事前分布に$N(0, 10)$、また$\beta_j$の事前分布に$N(1, 0.2)$を与えます。
# Initial values alpha_init <- rep(0.1, ncol(Y)) beta_init <- rep(0.1, ncol(Y)) theta_init <- rep(0.1, nrow(Y)) # Set anchors theta_init[which(rownames(Y) == "Ginsburg")] <- -2 # more liberal theta_init[which(rownames(Y) == "Scalia")] <- 2 # more conservative # RUN fit <- MH_irt(datamatrix = Y, # roll-call matrix alpha_init = alpha_init, # init for alpha beta_init = beta_init, # init for beta theta_init = theta_init, # init for theta MH_alpha = 2, # tuning param for alpha MH_beta = 0.6, # tuning param for beta MH_theta = 0.9, # tuning param for theta a0 = 0, # prior mean for alpha A0 = 10, # prior sd for alpha b0 = 1, # prior mean for beta B0 = 0.2, # prior sd for beta iter = 10000, # num of sampling warmup = 5000, # num of warmup thin = 10, # thining refresh = 1000, # Output the status of sampling every 1000 steps seed = 1) # seed
================================================================ Run Metropolis-Hasting Sampler for 2PL Item response model... Observations: 387 Number of individuals: 9 Number of items: 43 Total correct response: 190 / 387 [ 49 %] Priors: alpha ~ N(0, 10), beta ~ N(1, 0.2), theta ~ N(0, 1). ================================================================ Warmup: 1000 / 15000 [ 7 %] 2.4 sec Warmup: 2000 / 15000 [ 13 %] 4.9 sec Warmup: 3000 / 15000 [ 20 %] 7.5 sec Warmup: 4000 / 15000 [ 27 %] 10.3 sec Warmup: 5000 / 15000 [ 33 %] 12.5 sec Sampling: 6000 / 15000 [ 40 %] 14.6 sec Sampling: 7000 / 15000 [ 47 %] 16.7 sec Sampling: 8000 / 15000 [ 53 %] 18.7 sec Sampling: 9000 / 15000 [ 60 %] 20.8 sec Sampling: 10000 / 15000 [ 67 %] 22.3 sec Sampling: 11000 / 15000 [ 73 %] 23.5 sec Sampling: 12000 / 15000 [ 80 %] 24.8 sec Sampling: 13000 / 15000 [ 87 %] 26 sec Sampling: 14000 / 15000 [ 93 %] 27.2 sec Sampling: 15000 / 15000 [ 100 %] 28.5 sec Done: Total time 28.5 sec
終わりました。収束診断しますが、パラメータが多いので$\theta_i$だけ見てみます。
# Extract estimated thetas theta_iter <- fit$sample$theta %>% t() %>% as_tibble() # Convert into longer data theta_iter <- theta_iter %>% gather() %>% mutate(iter = rep(1:1000, times = nrow(Y))) # Plot theta_iter %>% ggplot(aes(iter, value)) + geom_line() + theme_bw() + xlab("Iteration") + ylab("") + facet_wrap(~ key, scales = "free_y")
大体イイ感じかと。それでは係数プロットを使って判事の理想点を可視化します。また、任命された政党のデータも追加してみました。
# Extract estimated theta theta <- fit$summary$theta # Plot theta %>% mutate(name = rownames(Y), party = c("Republican", "Republican", "Republican", "Republican", "Republican", "Republican", "Republican", "Democrat", "Democrat") %>% factor(levels = c("Republican", "Democrat"))) %>% ggplot(aes(y = reorder(name, mean), x = mean, color = party)) + geom_pointrange(aes(xmin = lwr, xmax = upr), size = 1) + theme_light() + xlab("Estimated Ideal Point") + ylab("") + theme(legend.title = element_blank(), legend.position = "bottom", legend.direction = "horizontal")
符号が反転してる感がありますが（通常、保守は右側でリベラルは左側）、それなりに妥当な理想点が推定できていると思います。
おわりに
余力があれば順序モデルや多項モデルに拡張していきたいですね。また、先ほどのMartin & Quinn (2002) で紹介されていたダイナミックな時変的な推定も実装してみたいですね。
実はCppで対数尤度関数を書く前に、全部Rで書いていたのですが結構遅くて、Cppに切り替えたら10倍以上速くなって感動しました。以上です。何か間違っていることがあればお知らせください。
*1:Clinton, J., Jackman, S., & Rivers, D. (2004). The statistical analysis of roll call data. American Political Science Review, 98(2), 355-370.
*2:Rosas and Shomer (2015) がこれらの取り扱いについて詳しく述べています。
*3:実際には、空間投票モデルやランダム効用理論を用いてIRTとの類似性を議論する必要がありますがここでは割愛します。
*4:Martin, A. D., & Quinn, K. M. (2002). Dynamic ideal point estimation via Markov chain Monte Carlo for the US Supreme Court, 1953–1999. Political analysis, 10(2), 134-153.
【R/Stan】潜在変数モデリングで潜在的に評価の高い南アジア料理の店を探す
突然ですが、最近のマイブームは都内の美味しい南アジア料理屋を探し回ることです。とはいっても、かなりの店舗さんが存在しますのでスパッと「ここいいかも～」みたいなお店を探し当てるのは中々苦労します。その中でも役に立つのが皆さんご贔屓の「食べログ」ですが、その評価スコアについて「点数の基準がようわからん」とか「何か点数にカラクリがあるんじゃね」のような疑念が絶えず向けられており、私自身も常に疑いながらdigってます。
そこで、いわゆる食べログスコアだけを参考にするだけではなくて「口コミ数」「ブックマーク数」「食事代」「立地」などの情報を利用することで潜在的な評価点を推定すれば、良いお店を探し当てることができるのでは？！とふと思い立ちました。ここで皆さんのお待ちかね、潜在変数モデルの出番ですよね。というわけで、今回もRとStanをこねくり回して潜在的に評価の高い南アジア料理屋さんはどこなのかを掘り当てていきます。
ちなみに、食べログのデータはサイトからスクレイプして持ってきたのですが、諸々説明してると長くなるので後程記事にしようと思います。気になる方はそちらをお読みください。今回はその辺端折ります、スミマセン。結果だけ知りたい人は下記の目次から飛んでください。
準備
まずは必要なパッケージとデータを読み込みます。スクレイプで取得したデータはsouthasia_data.RDataとして保存しました。
library(tidyverse) # データ加工 library(cmdstanr) # Stanを動かす library(posterior) # cmdstanの推定結果をハンドリングするやつ load("southasia_data.RData") # 南アジア料理屋の食べログ情報が入ったデータ
最近になってrstanからcmdstanrに乗り換えました。というのも、再コンパイルの必要がなかったりセッションがクラッシュすることが少なくなったりと色々なメリットがあったのでそうしました。また、WSL2でRstudio serverを動かすようになったので最近かなり快適なStanライフが送れてる気がします。
データの確認をしてみます。
dim(southasia_data)
[1] 1998 8
店舗数は全部で1998店舗といったところでしょうか。
head(southasia_data)
# A tibble: 6 × 8 name city area score nreview bookmark lunch_bud dinner_bud <chr> <chr> <chr> <dbl> <dbl> <dbl> <chr> <chr> 1 Kalpasi 世田谷区 千歳船橋 3.9 165 30774 ￥2,000～￥2,999 ￥3,000～￥3,999 2 シバカリーワラ 世田谷区 三軒茶屋 3.87 475 52270 ￥1,000～￥1,999 ￥1,000～￥1,999 3 カッチャル バッチャル 豊島区 新大塚 3.85 641 67299 ￥1,000～￥1,999 ￥3,000～￥3,999 4 砂の岬 世田谷区 桜新町 3.84 239 30972 ￥1,000～￥1,999 NA 5 やっぱりインディア 豊島区 大塚 3.83 415 24542 ￥1,000～￥1,999 ￥2,000～￥2,999 6 スパイスバル コザブロ 文京区 本駒込 3.83 159 15341 ￥1,000～￥1,999 ￥4,000～￥4,999
変数は以下の通りです。
name- 店舗名city- 市区町村area- 最寄り駅score- 食べログスコアnreview- 口コミ数bookmark- ブックマーク数lunch_bud,dinner_bud- 食事代 (ランチ、ディナー)
とりあえず、市区町村ごとにどれ程の店舗があるのかを確認してみます。せっかくなので東京都の地図上にプロットしてみましょう。{jpndistrict}パッケージ を利用すれば東京都のsfデータを取得することができます。
# 東京都の地図データ tokyo <- jpndistrict::jpn_pref(13) # 島嶼部を除外 tokyo <- tokyo[-(54:nrow(tokyo)), ] # 市区町村ごとに店舗数をカウント count_shop <- southasia_data %>% group_by(city) %>% summarise(n = n()) # プロット tokyo %>% left_join(count_shop, by = "city") %>% mutate(n = if_else(is.na(n), as.integer(0), n)) %>% ggplot() + geom_sf(aes(fill = n)) + theme_bw() + scale_fill_gradient(low = "white", high = "springgreen4", name = "Count") + ggtitle("Number of restaurants per municipality")
都心に相当集中してますが、意外と八王子にも郊外にしては店舗数がありますね。
生成モデル
潜在的評価をいかにして推定するかについて、以下の生成モデルを考えます。
\begin{align}
Y_{ij} \sim \mathcal{N}(\alpha_j + \beta_j \theta_i, \kappa_\mu).
\end{align}
$i = 1, \dots, I$とし、 料理店を表すインデックスとします。また、$j = 1, \dots ,3$は三つの評価項目を表し、「食べログスコア」「口コミ数」「ブックマーク数」です。$Y_{ij}$ は料理店$i$の評価項目$j$での獲得ポイントとします。
上式は、ほとんど項目反応理論 (IRT) の式形と同じです。$\alpha_j$は切片項で$\beta_j$は因子負荷量だとします。また、$\theta_i$がお店の潜在的評価です。IRT風に言えば、それぞれ「困難度」「識別度」「能力」といったところです。$\alpha_j$は項目のポイントを取りやすさを表すパラメータであり、$\beta_j$は潜在的評価$\theta_i$が高い店と低い店を切り分けるような項目のパラメータです。
ここで、項目のパラメータである$\alpha_j$, $\beta_j$は階層構造があることを仮定します。$c$を市区町村、$l$をランチの食事代カテゴリー、$d$をディナーの食事代カテゴリーとします。これらを導入することによって、評価項目のパラメータが市区町村やランチ・ディナー食事代カテゴリーごとに別々に生成されるようにします。さらに、市区町村ごとや食事代ごとによる項目評価の重みの違いなどを考慮したモデルになってます。具体的に書くと、
\begin{align}
\alpha_j &= \delta_{j} + \alpha_{cj} + \alpha_{lj} + \alpha_{dj},\\
\beta_j &= \gamma_{j} + \beta_{cj} + \beta_{lj} + \beta_{dj}.
\end{align}
となります。$\delta_{j}$ は評価項目 $j$ の全体平均項目難易度、$\alpha_{cj}$ は市区町村 $c$ における項目難易度、$\alpha_{lj}$ はランチ代カテゴリー$l$における項目難易度、$\alpha_{dj}$はディナー代カテゴリー$d$における項目難易度です。同様にして、$\beta$に関してもそれぞれの層ごとの識別度になります。
また、階層的な事前分布を以下で与えます。
\begin{align*}
\delta_j &\sim \mathcal{N}(0, 10), \ \ \ \gamma_j \sim \mathcal{N}(0, 10), \\
\alpha_{cj} &\sim \mathcal{N} (0, \kappa_{\alpha_C}), \ \ \ \beta_{cj} \sim \mathcal{N}(0, \kappa_{\beta_C}),\\
\alpha_{lj} &\sim \mathcal{N}(0, \kappa_{\alpha_L}), \ \ \ \beta_{lj} \sim \mathcal{N}(0, \kappa_{\beta_L}),\\
\alpha_{dj} &\sim \mathcal{N}(0, \kappa_{\alpha_D}),\ \ \ \beta_{dj} \sim \mathcal{N}(0, \kappa_{\beta_D}).
\end{align*}
$\kappa_{\alpha}, \kappa_{\beta}$はそれぞれの層ごとの標準偏差です。それぞれの層ごとに評価項目パラメータを生成します。また、潜在的評価$\theta_i$の事前分布を
\begin{equation*}
\theta_i \sim \mathcal{N}(0, 1).
\end{equation*}
とし、$\kappa_\mu$の事前分布を
\begin{equation*}
\kappa_\mu \sim Ga(1, 1).
\end{equation*}
とします。また、食べログスコア $S$と比較しやすくするため、$[min(S), max(S)]$の範囲で$\theta_i$を正規化します。
\begin{equation*}
\theta_i^\star = \frac{(\theta_i - min(\theta)) (max(S) - min(S)) }{max(\theta) - min(\theta)} + min(S).
\end{equation*}
これらをStanファイル上で記述してみます (tabelog.stan)。
data {
int N; //# of observations
int I; //# of shops
int J; //# of evaluation items
int C; //# of cities
int L; //# of lunch budget categories
int D; //# of dinner budget categories
int i[N]; //shop index
int j[N]; //evaluation item index
int c[N]; //city index
int l[N]; //lunch budget category index
int d[N]; //dinner budget category index
vector[N] Y; //evaluations
real max_tabelog; //maximum tabelog score for standardizing
real min_tabelog; //minimum tabelog score for standardizing
}
parameters {
vector[I] theta; //latent value
vector[J] delta; //mean difficulty
vector[J] alpha_C[C]; //city level difficulty
vector[J] alpha_L[L]; //lunch budget category level difficulty
vector[J] alpha_D[D]; //dinner budget category level difficulty
vector[J] gamma; //mean discrimination
vector[J] beta_C[C]; //city level discrimination
vector[J] beta_L[L]; //lunch budget discrimination
vector[J] beta_D[D]; //dinner budget discrimination
real<lower=0> sigma_aC; //sd for city level alpha
real<lower=0> sigma_aL; //sd for lunch budget level alpha
real<lower=0> sigma_aD; //sd for dinner budget level alpha
real<lower=0> sigma_bC; //sd for city level beta
real<lower=0> sigma_bL; //sd for lunch budget level beta
real<lower=0> sigma_bD; //sd for dinner budget level beta
real<lower=0> sigma_mu; //sd for evaluation score
}
transformed parameters {
vector[J] alpha; //difficulty
vector[J] beta; //discrinimation
vector[N] mu; //linear predictor
for (n in 1:N) {
alpha[j[n]] = delta[j[n]] + alpha_C[c[n], j[n]] + alpha_L[l[n], j[n]] + alpha_D[d[n], j[n]];
beta[j[n]] = gamma[j[n]] + beta_C[c[n], j[n]] + beta_L[l[n], j[n]] + beta_D[d[n], j[n]];
if (beta[j[n]] < 0) {
beta[j[n]] = beta[j[n]] * -1;
}
mu[n] = alpha[j[n]] + beta[j[n]] * theta[i[n]];
}
}
model {
//multilevel priors
for (cc in 1:C) {
alpha_C[cc] ~ normal(0, sigma_aC);
beta_C[cc] ~ normal(0, sigma_bC);
}
for (ll in 1:L) {
alpha_L[ll] ~ normal(0, sigma_aL);
beta_L[ll] ~ normal(0, sigma_bL);
}
for (dd in 1:D) {
alpha_D[dd] ~ normal(0, sigma_aD);
beta_D[dd] ~ normal(0, sigma_bD);
}
//priors
theta ~ std_normal();
delta ~ normal(0, 10);
gamma ~ normal(0, 10);
sigma_mu ~ gamma(1, 1);
//likelihood
Y ~ normal(mu, sigma_mu);
}
generated quantities {
//standardization
vector[I] theta_std;
theta_std = (theta - min(theta)) / (max(theta) - min(theta)) * (max_tabelog - min_tabelog) + min_tabelog;
}
Stanを動かす
それでは早速Stanによる推定に移っていこうと思います。ここで、Stanに送るためのデータが必要になってくるのでスパッと作っていきましょう。
正直必要のない作業だとは思いますが行列化した方が色々やりやすいので、とりあえずは先ほどのデータフレームを行列に変換します。また、口コミ数とブックマーク数はバラツキが非常に大きいので自然対数変換します。
mat <- southasia_data %>% mutate(ln_nreview = log(nreview), ln_bookmark = log(bookmark)) %>% select(name, score, ln_nreview, ln_bookmark) %>% as.matrix() sname <- mat[, 1] # 店舗名を抜き出す mat <- mat[, -1] # 一列目が店舗名列なので削除 mat <- apply(mat, 2, as.numeric) # なぜかcharacter matrix扱いになっているので全部数値に変換します rownames(mat) <- sname # 店舗名で行をラベリング
必要な変数を作り、リストにまとめます。
Y <- as.numeric(mat) # スコア、口コミ数、ブックマーク数をひとまとめ N <- length(Y) # 観測数 i <- rep(1:nrow(mat), times = ncol(mat)) # 店舗インデックス I <- max(i) # 店舗数 j <- rep(1:ncol(mat), each = nrow(mat)) # 項目インデックス J <- max(j) # 項目数 c <- rep(southasia_data$city_id, times = J) # 市区町村インデックス C <- max(c) # 市区町村数 l <- rep(southasia_data$lunch_bud_id, times = J) # ランチ代カテゴリーインデックス L <- max(l) #ランチ代カテゴリー数 d <- rep(southasia_data$lunch_bud_id, times = J) # ディナー代カテゴリーインデックス D <- max(d) # ディナー代カテゴリー数 max_tabelog <- max(southasia_data$score) # 食べログ最高スコア（標準化のため） min_tabelog <- min(southasia_data$score) # 食べログ最低スコア（同上） data <- list(N = N, I = I, J = J, C = C, L = L, D = D, i = i, j = j, c = c, l = l, d = d, Y = Y, max_tabelog = max_tabelog, min_tabelog = min_tabelog)
次に、上記で作成したtabelog.stanをコンパイルします。
model <- cmdstan_model("tablelog.stan", cpp_options = list( stan_threads = TRUE # スレッド数を指定 ))
読み込めたので分析を実行していこうと思います。普通のサンプリングだと計算がかなり遅いので、今回は自動変分ベイズ (ADVI) で計算スピードを爆上げします。モデル名$variationalで{cmdstanr}でADVIを実装できます。
fit <- model$variational(data, seed = 1, threads = parallel::detectCores())
推定には10秒もかからなかったと思います。結果を抽出していきます。{cmdstanr}ではfit$summary("パラメータ")で任意の推定値を抜き出すことができますが、デフォルトで90%区間しか取ってきてくれないので95%が欲しいときは自力で計算する必要があります。fit$draws("パラメータ")で近似分布からのパラメータ推定値 1000個 (デフォルト) を抜き出してくれます。その推定値を基にして、95%信用区間を計算していきます。まず、下側・上側を計算する関数を定義します。
lower <- function(x) quantile(x, probs = .025) upper <- function(x) quantile(x, probs = .975)
潜在的な評価である$\theta_i$を$[min(S), max(S)]$範囲で正規化したパラメータである$\theta_i^\star$の推定値を抜き出してみましょう。
theta <- fit$draws("theta_std") theta_est <- tibble(name = sname, station = southasia_data$area, city = southasia_data$city, lunch_bud = southasia_data$lunch_bud, dinner_bud = southasia_data$dinner_bud, lwr = apply(theta, 2, lower), med = apply(theta, 2, median), upr = apply(theta, 2, upper), tabelog_score = southasia_data$score)
結果
とりあえず推定指標と食べログスコアの相関をプロットしてみます。
cor <- cor.test(theta_est$med, theta_est$tabelog_score) theta_est %>% ggplot(aes(x = med, y = tabelog_score)) + geom_point() + theme_bw() + xlab("Estimated latent score") + ylab("Tabelog score") + annotate(geom = "text", label = paste("italic(r) == ", round(cor$estimate, 3)), x = 3.75, y = 3.2, parse = TRUE)
まあ、特に何か得られるわけではないですがある程度の相関はありそうです。それでは推定から得られた潜在的に評価が高い南アジア料理店トップ20を以下に発表していこうと思います。
| 順位 | 店舗名 | 最寄り駅 | 潜在的評価 | ランチ代 | ディナー代 |
|---|---|---|---|---|---|
| 1 | コチン ニヴァース | 西新宿五丁目 | 3.900 | NA | ￥1,000～￥1,999 |
| 2 | ケララバワン | 練馬 | 3.869 | ￥1,000～￥1,999 | ￥2,000～￥2,999 |
| 3 | シャングリーラ 蒲田店 | 蒲田 | 3.851 | ～￥999 | ￥1,000～￥1,999 |
| 4 | カッチャル バッチャル | 新大塚 | 3.849 | ￥1,000～￥1,999 | ￥3,000～￥3,999 |
| 5 | タンドールバル カマルプール 木場店 | 木場 | 3.847 | ￥1,000～￥1,999 | NA |
| 6 | 南印度ダイニング ポンディバワン 武蔵新田 | 武蔵新田 | 3.846 | ～￥999 | ￥2,000～￥2,999 |
| 7 | ハリマ・ケバブ・ビリヤニ | 稲荷町 | 3.830 | ～￥999 | ￥2,000～￥2,999 |
| 8 | スパイスカフェ | 押上 | 3.817 | ￥1,000～￥1,999 | ￥6,000～￥7,999 |
| 9 | アーンドラ・キッチン | 御徒町 | 3.815 | ～￥999 | ￥2,000～￥2,999 |
| 10 | クンビラ | 恵比寿 | 3.808 | ～￥999 | ￥4,000～￥4,999 |
| 11 | シバカリーワラ | 三軒茶屋 | 3.806 | ￥1,000～￥1,999 | ￥1,000～￥1,999 |
| 12 | サルマ ティッカアンドビリヤニ | 品川 | 3.791 | ～￥999 | ￥2,000～￥2,999 |
| 13 | カリーライス専門店エチオピア 本店 | 神保町 | 3.789 | ￥1,000～￥1,999 | ～￥999 |
| 14 | カーン・ケバブ・ビリヤニ | 新橋 | 3.786 | ～￥999 | ￥2,000～￥2,999 |
| 15 | ネパール民族料理 アーガン | 新大久保 | 3.785 | ～￥999 | ￥2,000～￥2,999 |
| 16 | ダバ インディア | 京橋 | 3.780 | ￥1,000～￥1,999 | ￥2,000～￥2,999 |
| 17 | ヴェヌス サウス インディアン ダイニング 錦糸町店 | 錦糸町 | 3.778 | ￥1,000～￥1,999 | ￥1,000～￥1,999 |
| 18 | タンブリン カレー&バー | 北千住 | 3.777 | ￥1,000～￥1,999 | ￥2,000～￥2,999 |
| 19 | Sajilo Cafe | 吉祥寺 | 3.775 | ￥1,000～￥1,999 | ￥1,000～￥1,999 |
| 20 | アーンドラ・ダイニング 銀座 | 銀座一丁目 | 3.773 | ～￥999 | ￥2,000～￥2,999 |
うーん。妥当な順位なのかわからんな～。実際に推定された指標の妥当性を確かめる方法は実際に食べるしかないので、このリストに上がってきたってことで行ってみようっていう気にはなりました。
結論を言うと、何もわかりませんでした！
おわりに
生成モデルを作って都内南アジア料理店の潜在的評価を推定してみましたが、結局数値だけ見ても何もわからないので実際に足を運んで確かめるべしという素晴らしい知見を得ることができました。
ちなみに、私の推しは清澄白河にあるナンディニさんと西早稲田のアプサラさんです。前者は平日のミールスセットが素晴らしくて後者はバナナリーフのスリランカカレーが最高においしいです。最近ミールスに異常にハマっているので良いお店があれば知らせてください。以上。
ベストバイ2021
はじめに
こんにちは。長らくブログを更新していませんでした、お久しぶりです。卒業論文執筆を終えて心的・時間的余裕が出てきたので何か書こうかな～と思い立ち、とりあえず今年買ってよかったものを紹介していこうと思います。いつもとは毛色が異なってくると思いますが、番外編的な感じで緩くやっていきます。とはいっても、このブログを始めたのは「勉強」と「趣味」を淡々と記していこうという動機だったので、今回の記事は「趣味」方面にあたるわけで、ブログの趣旨からは逸脱していないかと。まあ、ともかく長い前置きはこれくらいにして早速紹介していこうと思います。ここからは「アパレル編」「書籍編」に分けてお送りします。
アパレル
適当に今年買った服や服飾品の中で良かったと思うものを紹介します。
INDIVIDUALIZED SHIRTS (Urban Research Doors 別注) - B.D. OX Shirt
今年の3月で閉店したUrban Research Doors 池袋パルコ店の閉店セールで買った。実は他の服が目当てだったが、「お、これめちゃくちゃいいな」と思い試着してみるとタイトすぎずルーズすぎずのベストシルエットで即購入。かなりお気に入りで頻繁に着ているので、もう既にOXシャツ特有のフェード感が出始めてる。まあ、それがOXシャツの醍醐味だと思いますが。ちなみに、これが初めてのインディヴィ。今度、神宮前のUsonian Good Storeさんでも覗いて、良いインディヴィのシャツ買いたいな～。
Pendleton - BW pattern 3B wool jacket (40-50's vintage)
高円寺の某チェーン古着屋で叩き売られているところを勇敢に助けてあげた一着。これもインディヴィのシャツ同様にブラックウォッチパターンであり、このままだとBW柄大好き芸人になってしまう。40-50年代のヴィンテージにもかかわらず、ほぼNOSの状態で店頭に並んでおり、なぜ売れていなかったのかと疑問を呈してしまうほどだ。逆に考えてみると、いわゆるヴィンテージショップではなく高校生～大学生向けの比較的安価な古着が置かれている古着屋だから売れなかったのかもしれない（安価古着と比べるとちょっと高めの値段ではあったが、それでも余裕で相場割れする値段）。ペンドルトンのウールのチェックジャケットが結構好きなので割と着用する機会が多いが、着るか着ないかを別にしてもコレクションとして持っておきたい一着。
Incubus - Band tee (2002)
高円寺のLeeLooさんで購入したTee。©2002の表記が入っており、おそらく"Make Yourself"のツアーのマーチかと。90~00's前半のニューメタルやポストグランジ系のマーチが欲しすぎて血眼になって色々ネットを検索していた時にドンピシャに見つけた。2000年代に入ってからのボディではあるが、サイズ感やノリは90年代のGiantに負けず劣らずで嬉しい。ちなみに、Incubusで一番好きな曲はDigです（もちろんMake Yourselfの曲も良い）。
Static-X - Bootleg band tee (1999)
高円寺のSafari 4号店さんで購入（また高円寺だ…）。おそらく当時のオフィシャルマーチではなくブートだと思われる。でもブートの方がオフィシャルより良いデザインのものが多いなあ～と感じることがそこそこある。前面にWisconsin Death Trip (1999) のアートワークをドカンとプリントしたTeeなので存在感もあるし、何よりもイケてる。ほぼボロに近い状態のフェード感とプリント割れが凄まじいが、それも味がある。自分のポリシーとしてルーツのバンドのTeeしか着ないというものがあるので、これに出会えたのは中々嬉しい出来事。ちなみに、店舗に行ってTシャツの山から掘り当てたのだが、一緒に行ったパートナーもDeftonesのTeeを掘り当てていたのでSafari4号店は意外とニューメタル的穴場かもしれない。
Standard Jounal - Tote bag by Ken Kagami
表参道のJournal Standardで購入。私は普段からリュック派なのでトートバッグとはほぼ無縁であり、人の買い物に付き合って店舗に行っただけだったが、この「ジャーナル」という何ともシュールな文字列とフォントに加えて 46.5×45 という比較的大きめなサイズに完全に捕まってしまい、あっさり購入。使い勝手もよく、アンチトートバッグだった時がバカバカしく思えるほど使いまくってる。使いすぎて至る所にシミができてしまった。ちなみにこの"Standard Journal"は、Journal Standardがデザイナーの方々とコラボした商品を出しているプロジェクトらしい。で、このトートはアーティストの加賀美健さんがデザインしたものらしい。B4のうちに論文をジャーナルに投稿するという目標達成祈願も込めて、この「ジャーナル」トートを使い続けよう。
書籍
次に書籍を紹介します。
谷崎潤一郎『痴人の愛』
ここ何年かで読んだ小説の中で群を抜いて魅せられてしまった一冊。小説というよりも、一人称視点からそのまま語られる「私小説」といった方が良いのか。マゾヒズム的な狂愛、美と悪への執着といったいわばサブカル的な側面が強く、是非が分かれる作品ではあるが、その異質さというか異常さに惹かれた。ページ数は多いものの、とても読みやすく半日あれば読み終わる。が、男が読むとお腹が痛くなる作品ではある。この記事はあくまで買ったもの一覧であり書評ではないのでこれくらいにしておきたい。ちなみに、購入したときに「某芸能人オススメの一冊！」のようなコピーが入った帯が付いていたのだが、正直その帯を見た「ウワッ」と思い瞬間買うか否か迷ってしまった。そういう本ほど読みたくなくなるのはなんでだろうか、でも買って読んだ。
Angrist, J. D., & Pischke, J. S. Mostly harmless econometrics.
https://www.amazon.co.jp/dp/0691120358/ref=cm_sw_r_tw_dp_ACP11718N38MT9NYKBK7www.amazon.co.jp
夏に購入。この本のせいで因果推論の沼に嵌まり込んでしまった。Less mathで読みやすいとはいえ、証明の多くがスキップされているので逆に後追いするのは大変だった。また、夏にあったMITの某先生が開講している集中授業の教科書でもあり、その授業は中々地獄であったため、当時を思い出してしまいお腹が痛くなるという側面もある。今でもたまにパラパラ読み返しては、「計量経済わからん」状態になる。翻訳版もあるらしいが、Twitter上では「翻訳版は読みにくいので原本の方がよい」という声も聴く。著者の一人であるAngristがノーベル経済学賞を取ったのはとてもタイムリー。
シンコー・ミュージック『ラウド・ロック CDガイド』
神保町のブンケンロックサイドさんで購入したムック本。90年代のニューメタル始めスカ～NYHCからグラインドまで幅広く紹介されている。ラウドロックというと少々幼稚なイメージが出てしまうが、そんなものがどうでもよくなるくらいの250ページに渡る情報量で圧倒される。最初は「マイナーなミクスチャーとかニューメタルが掘れればいいな」と軽く思っていたのだが、それどころではなくて笑ってしまう情報量である。海外のバンドだけでなく、宇頭巻やBACK DROP BOMBなどのJapaneseミクスチャーも紹介されているので非常に信頼できる。Bandcampなどを使って色々探すのもアリだが、もう存在しないバンドなどを探すのは困難なため、このような本は非常に助かるし読んでいて面白い。1999年発売らしい。もう手に入るかはわからない。
おわりに
だらだらと書きましたが、ベストバイというよりも作品紹介のブログみたいになってしまって何だか洒落た感じがでなくてちょっぴり悲しい限りです。とはいえ、ただの買ったもの紹介だけというどうでもいい内容にお付き合いいただいてありがとうございます。来年はちゃんと音楽や統計とかの記事も書きます。書きます。書きます。書け。論文も書きます。
【R】Spotify APIを利用して関連するアーティストをDigりまくる
今回は、Spotify APIを利用してデジタルにdigをしてみます。目次は以下の通りです。
はじめに
先日、「SpotifyのAPI利用をRでできねーかなー」とか思っていたら、まさにドンピシャのパッケージ {spotifyr} を発見しました。
（Pythonには{spotipy}ならぬ同じようなパッケージが存在しますが、それに比べてこのパッケージのネーミング微妙じゃね？と思いました。）
何をするのか
ともあれ、今回はこのRパッケージを使って「関連するアーティスト」のネットワークを可視化する作業をやってみたいと思います。上手く可視化できれば何千もの関連するアーティストを一気にDigれるので、音楽オタクの皆様にはとても最適な内容です。
パッケージの読み込み+α
まずは、作成者であるcharlie86氏のGitHubページに倣ってパッケージをインストールしましょう。私の確認では、このパッケージはCRAN上にないので、GitHub上からでしかインストールできないっぽいです。
devtools::install_github("charlie86/spotifyr")
次にパッケージを読み込みます。今回使用するパッケージは以下の通りです。
library(tidyverse) # 実家のような安心感 library(spotifyr) # 今回のメイン library(igraph) # ネットワーク分析で重宝するパッケージ library(tidygraph) # グラフデータをtidyに library(ggraph) # ggplot2でグラフ
また、SpotifyのAPIを利用するためにはdeveloper登録をする必要がありますので事前に済ませておいてください。登録は以下のブログが参考になると思います。
登録が完了したらClient IDとClient Secretを確認します。それらをRに以下のように貼り付けてください。
Sys.setenv(SPOTIFY_CLIENT_ID = "Your client ID") Sys.setenv(SPOTIFY_CLIENT_SECRET = "Your client secret")
アーティスト情報の取得
次に、今回の肝である関連するアーティスト情報の取得を行っていきましょう。
まずは、起点となる最初のアーティストの情報を取得していきます。これは別に何でもいいのですが、最近小中学生の時にドハマりしていた音楽ブームが個人的に巻き起こっているのでとりあえず ``My Chemical Romance"でやってみます。ちなみに、マイケミで一番好きな曲はDisenchantedです。
それでは早速やっていきましょう。
まずは、マイケミのSpotify上でのIDを取得していきます。search_spotify関数で該当するアーティスト情報を抜き出します。
search <- search_spotify("my chemical romance") id <- search$artists$items$id[1] # 有名なアーティストならばid変数のの1要素目 artist_name <- search$artists$items$name[1] # 後で使うので一応名前も抜く
次にget_related_artists関数で「関連するアーティスト」を抜き出していきます。デフォルトだと最大で20組が抜き出されます。
related <- get_related_artists(id) related_name <- related$name # 名前を抜く related_id <- related$id # IDを抜く related_name
[1] "The Used" "The Red Jumpsuit Apparatus" "Yellowcard" [4] "Hawthorne Heights" "The All-American Rejects" "Good Charlotte" [7] "Frank Iero" "All Time Low" "Mayday Parade" [10] "Simple Plan" "Senses Fail" "Escape the Fate" [13] "AFI" "Fall Out Boy" "Jimmy Eat World" [16] "Silverstein" "Falling In Reverse" "Panic! At The Disco" [19] "Pierce The Veil" "Angels & Airwaves"
P!ATDやThe Usedなど当時のアーティストの中にPierce The VeilやFalling In Reverseなんかが紛れ込んでいるんですね。先日、PTVのKing for a dayのMVを超久しぶりに見たら再生数1億回超えてて狂ってましたね。懐かしすぎて中1の頃が偲ばれます。あと実はKellin Quinnってもう35歳らしいですよ。年齢不詳だな～。
話題が完全にそれてしまいましたが、今抜き出した値を「検索アーティスト」「関連するアーティスト」に対応するようにデータフレームに格納します。
data <- tibble(artist_name, related_name) data_id <- tibble(artist_name, related_id) head(data)
# A tibble: 6 x 2 artist_name related_name <chr> <chr> 1 My Chemical Romance The Used 2 My Chemical Romance The Red Jumpsuit Apparatus 3 My Chemical Romance Yellowcard 4 My Chemical Romance Hawthorne Heights 5 My Chemical Romance The All-American Rejects 6 My Chemical Romance Good Charlotte
それでは、早速「関連するアーティスト」の「関連するアーティスト」を抜き出してみましょう。まずは、分析しやすくするためにsearch_relate関数を定義します。
search_related <- function(id) { artist <- get_artist(id) artist_name <- artist$name related <- get_related_artists(id) related_name <- related$name related_id <- related$id data <- tibble(artist_name, related_name) data_id <- tibble(artist_name, related_id) return(list(data = data, data_id= data_id, related_id = related_id)) }
検索IDを入れれば、勝手に「検索アーティスト」「関連するアーティスト」のデータフレームと「検索ID」「関連ID」データフレーム、さらに「関連ID」ベクトルを含むリストを返してくれます。
次にこの関数をマイケミの関連するアーティスト20組にそれぞれ適用し、新たに202 = 400組を抜き出してみます。正直、for文だと遅いのでmapで処理したかったところですが、なぜかmapだと上手く取得しきれなかったので仕方なくfor文で行きます。これを実行すれば、一番最初に作成した「マイケミ」「関連するアーティスト」データフレームにどんどん新たにアーティストが追加されていきます。
今回は、あまりデータが莫大になりすぎると大変なので、3回の繰り返しだけにします（つまりマイケミの「関連するアーティスト」の「関連するアーティスト」の「関連するアーティスト」の「関連するアーティスト」まで）。
# 1回目 for (i in 1:length(related_id)) { out <- search_related(related_id[i]) if (exists("df_relate") == TRUE) { df_relate <- bind_rows(df_relate, out$data) } else{ df_relate <- bind_rows(data, out$data) } if (exists("df_relate_id") == TRUE) { df_relate_id <- bind_rows(df_relate_id, out$data_id) } else{ df_relate_id <- bind_rows(data_id, out$data_id) } } # ここで重複ペアを消す df_relate_id_2 <- df_relate_id[-(1:20), ] %>% mutate(pair = paste0(artist_name, related_id)) %>% distinct(pair, .keep_all = TRUE) %>% select(-pair) # 2回目 for (i in 1:nrow(df_relate_id_adj)) { out <- search_related(df_relate_id_adj[i, 2]) if (exists("df_relate2") == TRUE) { df_relate_2 <- bind_rows(df_relate_2, out$data) } else{ df_relate_2 <- bind_rows(df_relate, out$data) } if (exists("df_relate_id_2") == TRUE) { df_relate_id_2 <- bind_rows(df_relate_id_2, out$data_id) } else{ df_relate_id_2 <- bind_rows(df_relate_id, out$data_id) } } # 前の420組のペアリスト削除したいので、まずはリストを作る pair_list <- df_relate_id %>% mutate(pair = paste0(artist_name, related_id)) %>% select(pair) %>% as.matrix() %>% as.character() # filter関数では複数のマッチに対して補集合を返すものがない（というか知らない）ので定義する `%notin%` <- Negate(`%in%`) # 削除 df_relate_id_2_adj <- df_relate_id_2[-c(1:420), ] %>% mutate(pair = paste0(artist_name, related_id)) %>% filter(pair %notin% pair_list) %>% distinct(pair, .keep_all = TRUE) %>% select(-pair) # 3回目 for (i in 1:nrow(df_relate_id_2_adj)) { out <- search_related(df_relate_id_2_adj[i, 2]) if (exists("df_relate_3") == TRUE) { df_relate_3 <- bind_rows(df_relate_3, out$data) } else{ df_relate_3 <- bind_rows(df_relate_2, out$data) } if (exists("df_relate_id_3") == TRUE) { df_relate_id_3 <- bind_rows(df_relate_id_3, out$data_id) } else{ df_relate_id_3 <- bind_rows(df_relate_id_2, out$data_id) } } # さいごに重複を削除 df_relate_3 %>% mutate(pair = paste0(artist_name, related_name)) %>% distinct(pair, .keep_all = TRUE) %>% select(-pair) -> df_net df_relate_id_3 %>% mutate(pair = paste0(artist_name, related_id)) %>% distinct(pair, .keep_all = TRUE) %>% select(-pair) -> df_id_net # 一応保存 write.csv(df_relate_3, "relate_name.csv", row.names = FALSE) write.csv(df_relate_id_3, "relate_id.csv", row.names = FALSE)
脳筋的に抽出を繰り返してしまいましたが、あまりよろしくない実行だと思います。もっといいやり方を見つけて改定したいです。
ともあれ、無事に抜き出し終わりました。データを確認してみましょう。
length(unique(df_net$artist_name))
[1] 557
length(unique(df_net$relate_name))
[1] 2100
まあまあの数のアーティストを取得することができました。可視化したらどうなるやら。
ネットワークの可視化
本題に移ります。まずは、先ほどのdf_netをグラフ用（igraphオブジェクト）に変換します。
g <- graph.data.frame(df_net, direct = FALSE) # dataframe → graph data g <- simplify(g, remove.multiple = TRUE, remove.loops = TRUE) # 重複や自己ループを削除 g_tbl <- as_tbl_graph(g, directed = FALSE) # tidyに
それでは、{ggraph}パッケージを用いてネットワークを可視化します。
g_tbl %>% ggraph(layout = "kk") + geom_edge_link(alpha = .6, color = "black", width = .01) + geom_node_point(size = .001, alpha = .5) + geom_node_text(aes(label = name), size = .4, nudge_y = .26) + theme_minimal() + scale_x_continuous(breaks = NULL) + scale_y_continuous(breaks = NULL) + xlab("") + ylab("")
なんだか面白そうなグラフになりました。何がどうなっているのか全く分かりませんが。一番密集しているところを見てみましょう。
何やら2000年代前期に流行ったemoメンツが勢ぞろいですね。
少し外れたところを見てみると、LOATHEやVoid of Visionといった流行りのメタルコアバンドなんかも視認できます。
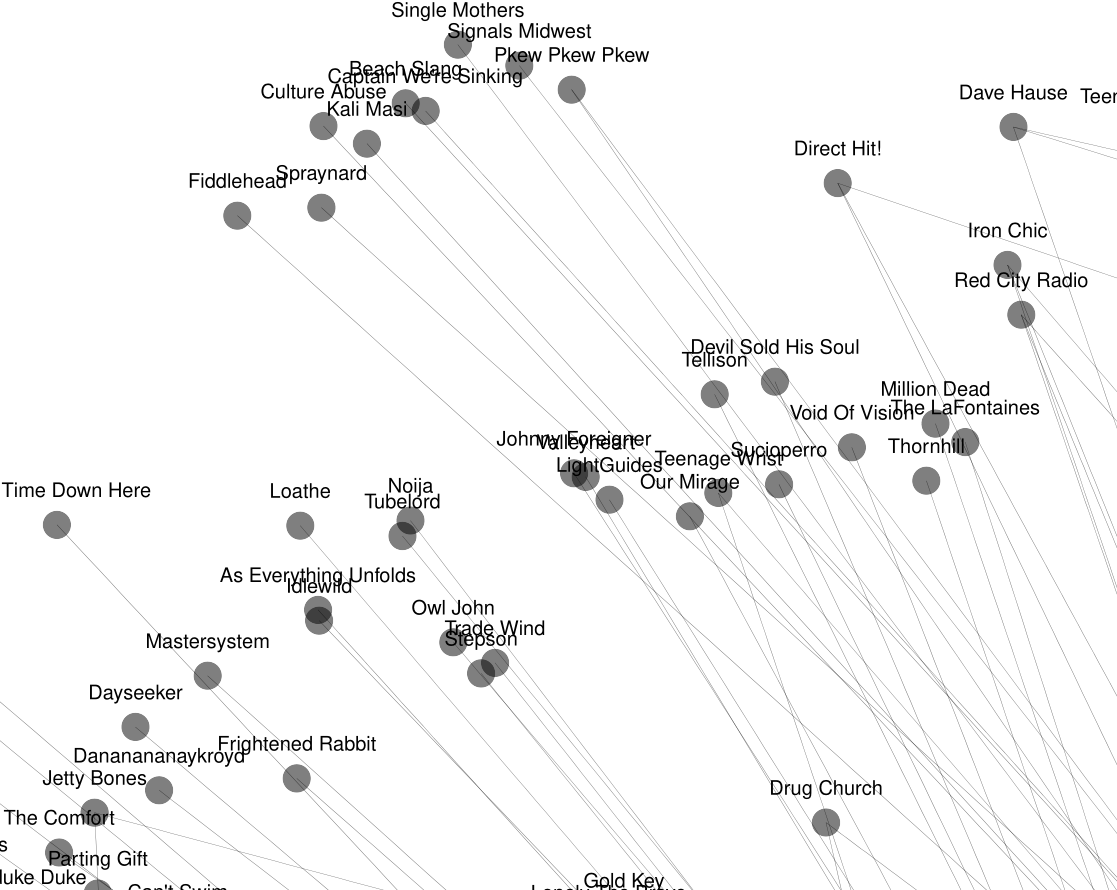
中でも、一番驚いたのがこれ。
なんと末端の方を見ると謎に鬱Pや八王子PなどのボカロPやDECO*27までもいるんです。なんで？マイケミから鬱Pまでの経路を調べてみましょう。
get.shortest.paths(g_tbl, "My Chemical Romance", "Utsu-P")$vpath
[[1]] + 5/2102 vertices, named, from 8f3234d: [1] My Chemical Romance Frank Iero Mindless Self Indulgence Maretu [5] Utsu-P
これ結構衝撃的なのが、Frank Ieroを通ってエレクトロ方面に流れて鬱Pまでたどり着いているようですね。また、ネットワーク分析的Digの醍醐味（？）ですが、新たに ``Mindless Self Indulgence Maretu" というアーティストを知ることができました。あまり好みではなかったですが。
実際のところ、媒介性が一番大きいアーティストを調べてみると
between <- as.matrix(betweenness(g_tbl)) between[which(between == max(between)), ]
Frank Iero
246394.4
Frank Ieroなんですよね。すげー。マイケミからネットワークをスタートさせてマイケミメンバーの媒介力を知るというね。
